- Historique
- L’astrolabe
Instrument de calcul inventé par Hipparque (astronome grec du 2ème siècle avant J.C.) permettant d’établir les relations entre la position des étoiles et le temps. Son développement par les Arabes fut lié aux nécessités du culte pour connaître les heures de lever et coucher du soleil, de son passage au méridien et à une hauteur donnée l’après midi (pour fixer les heures des prières).
Le plus ancien instrument date de l’an 315 de l’Hégire (927-928 ap. J.C.) et se trouve au Musée National du Koweit. Des exemplaires des XVI ème et XVII ème siècle se trouvent au Musée des Arts et Métiers à Paris.
- Différents types
Il existe différents types d’astrolabes (sphérique, plan équatorial, plan universel) mais le plus courant est l’astrolabe planisphérique qui est une projection plane équatoriale de pôle sud de la sphère céleste.
- L’astrolabe
- Le système de représentation
- Le problème de la représentation
Le problème de réaliser une carte c’est à dire de faire correspondre les points d’une sphère à ceux d’un plan date de l’Antiquité. Aucune solution respectant partout à la fois surfaces, angles (La sphère étant une surface non développable) ne peut être trouvée à ce problème.
La méthode la plus ancienne consiste à projeter l’image de la sphère terrestre ou céleste sur une feuille plane (projection planisphérique), roulée en cylindre (projection cylindrique) ou en cône (projection conique).
Le projecteur peut-être au centre (centrale), à l’infini (orthographique) ou être un des points de la sphère (stéréographique ou projection d’Hipparque qui vécut vers 150 avant J.C.).
Certaines projections respectent les surfaces (projections équivalentes), d’autres conservent les angles (projections conformes). De nombreuses représentations modernes utilisant l’ordinateur ne sont ni équivalentes, ni conformes.
- Intérêt d’une
carte respectant les angles sur une carte de la terre
La représentation de Gerardus Mercator (Gerhard Kremer: Flandres 1512, Duisbourg 1594)
Carte de Terre Sainte (1537), du monde (1538), des Flandres (1540), du globe (1540), de la sphère céleste (1551), carte de “Mercator” (1569), projection cylindrique déformée pour obtenir une représentation conforme.
Principe:
Depuis l’introduction de la boussole dans la navigation on dirigeait les navires suivant une route, appelée loxodromie, coupant les méridiens à angle constant. Ainsi pour aller d’un point A à un point B, il suffit de déterminer le cap à prendre et de le suivre pendant tout le voyage à l’aide de la boussole.
Pour se rendre compte de la position du navire il faut pouvoir tracer simplement sur la carte le chemin parcouru: la carte la plus intéressante serait alors une carte dont la loxodromie serait représentée par le segment de droite AB.
Pour cela il faut que les angles soient conservés. Les angles sont conservés si un petit cercle de la sphère est transformé en un petit cercle du plan, c’est à dire si les dilatations de longueurs en un point sont les mêmes dans toutes les directions.
La représentation de Mercator part d’une projection cylindrique (dilatant donc les parallèles en 1/cosf, si la latitude est f) et l’on dilate ensuite les méridiens en 1/cosf pour que les dilatations des parallèles et des méridiens soient les mêmes. Les longueurs ne sont par conséquent plus respectées ni les surfaces.
- Projection stéréographique
plane équatoriale de pôle Sud
Historique: La projection d’Hipparque (150 av J.C.), est décrite par Ptolémée (2ème siècle après J.C.)
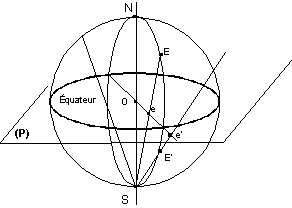
Principe: Soit la sphère céleste, N le pôle céleste Nord, S le pôle céleste Sud.
À une étoile E, on fait correspondre l’étoile e, point d’intersection de ES avec le plan équatorial.
La projection du cercle équatorial sera lui-même, la projection e d’un astre E de l’hémisphère nord sera située à l’intérieur du cercle équatorial, la projection e’ d’un astre E’ de l’hémisphère Sud sera à l’extérieur.
Intérêt
1) Conservation des angles donc des formes des petites constellations
2) De plus la projection d’un grand cercle de la sphère est un grand cercle du plan (P)
- Le problème de la représentation
- Projections de cercles
particuliers dans la projection stéréographique
- Projection des cercles passant
par N et S (Cercles méridiens d’égale
ascension droite)
Les images sont des droites passant par O
- Projection des cercles parallèles
au plan de projection (P)
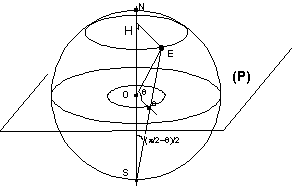
Les cercles parallèles ont pour image des cercles concentriques de centre O
Un point E se trouvant à l’intersection d’un cercle parallèle de déclinaison q et d’un 1/2 cercle méridien d’ascension droite a se trouvera en projection à l’intersection d’une demi-droite et d’un cercle.
Soit a le rayon de la sphère céleste: OE= a
OH=asinq HE=acosq Oe/HE= SO/SH d’où Oe=acosq * a/(a+asinq) = acosq/(1+sinq) = atg(p/4-q/2)
On peut aussi dire directement Oe= atg((p/2-q)/2) = atg(p/4-q/2) car l’angle inscrit en S dans le triangle HSE vaut la moitié de l’angle au centre en O dans le triangle HO
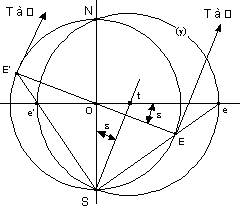
- Projection (g) d’un cercle quelconque (G)
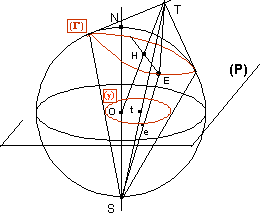
 Soit
le cercle (G) de centre H et E un point du cercle. Soit (g) la projection
de (G) sur (P)
Soit
le cercle (G) de centre H et E un point du cercle. Soit (g) la projection
de (G) sur (P)
Soit la droite perpendiculaire au cercle (G) et tangente à la sphère. Elle coupe la droite OH en un point T, et TE se projettera en te sur le plan de projection. Pour un point E’, la projection de TE’ donnera te’.
Or la projection stéréographique conserve les angles, donc la projection d’une normale à (G) est une normale à (g). La projection (g) de (G) est donc une courbe dont toutes les normales passent par un point fixe t. Seul le cercle centré en t convient: (g) est donc ce cercle centré en t.
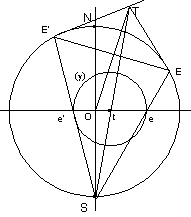
Pour construire ce cercle, on fait pivoter dans le plan de la feuille de tracé
* le plan SET * le plan (P) de projection Alors on obtient E projeté en e et E’ projeté en e’
Cas particulier d’un cercle passant par O
Soit un cercle passant par O d’inclinaison e par rapport au plan (P)
Le centre t du cercle projeté se trouve en traçant la droite passant par S parallèles aux tangentes en E et E’
Donc Ot = atge r = St = a/cose
- Projection des cercles passant
par N et S (Cercles méridiens d’égale
ascension droite)
- Construction de tympan
de l’astrolabe (Partie fixe)
- Projection des cercles verticaux passant par Zénith
et Nadir d’un lieu à la latitude f
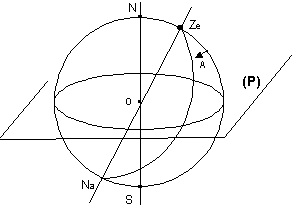
Les projections déterminées graphiquement
* Un vertical est un demi-cercle passant par zénith et nadir du lieu, repéré par son azimuth A par rapport au méridien céleste Sud NS.
* Les projections de Ze et Na étant z et n, la projection du vertical est donc un cercle passant par n et z.
* De plus la projection du méridien Nord Sud est Os.
En Ze le vertical Ze-Na fait l’angle A avec le méridien N-S; en z projection de Ze les projections du vertical et du méridien feront aussi l’angle A, ce qui permet de trouver le centre w.
Les projections déterminées par le calcul
Oz=atg(p/4-f/2) et On=acotg(p/4-f/2) (Voir II.4.) donc nz = atg(p/4-f/2) + a/tg(p/4-f/2)= 2a/cosf
tg A= Iz/wI donc wI = Iz / tgA=a/cosftgA et le rayon du cercle cherché vaut R(A)=wz= Iw/cosA=a/cosfsinA
On peut ainsi tracer tous les verticaux à partir de leur centre w en faisant varier l’azimuth A de 0° à 180°
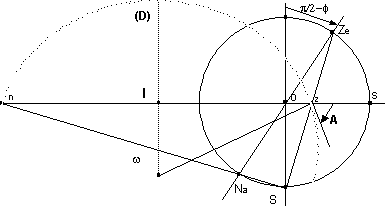
Pour la latitude f = 45°
Pour construire un astrolabe tenant sur un format A4, on prend a=5
Oz = atg(p/4-f/2) = 2,032 Iz = a/cosf = 7,071 Iw= 7,071/tgA R(A) = 7,071/sinA
Azimuth A
0
10
20
30
40
50
60
70
80
90
100
Iw(A)
°
40,10 19,43 12,25 8,43 5,93 4,08 2,57 1,25 0,00 -1,25 R(A)
°
40,72 20,67 14,14 11,00 9,23 8,16 7,52 7,18 7,07 7,18
Les graduations en azimuth vont de 0° (Sud), 90° (Ouest), 180° (Nord), 270° (Ouest) à 360°
- Projection des demi-cercles horaires (demi-cercles passant
par N et S)
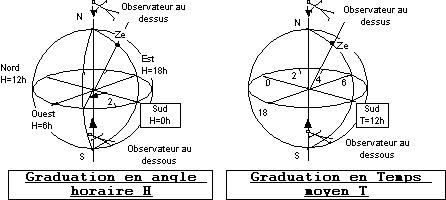
Les projections: D’après III1 ce sont des demi-droites passant par O
Les graduations: On sait que l’angle horaire représente l’angle entre le demi-méridien céleste et le méridien sud avec un choix d’unité d’angle appelé l’heure valant 15°. L’angle horaire du méridien Sud est H=Oh, celui de l’Ouest 18h, celui du Nord 12h, celui de l’Est 6h.
Le pourtour du tympan sera gradué en H +12heures (Temps solaire moyen)
Le choix de H +12 heures est fait pour que lorsqu’un astre passe au méridien la valeur lue soit 12h et non 0h.
Le sens de graduation est - positif si l’observateur est au dessous de (P)
- rétrograde si l’observateur est au dessus de (P)
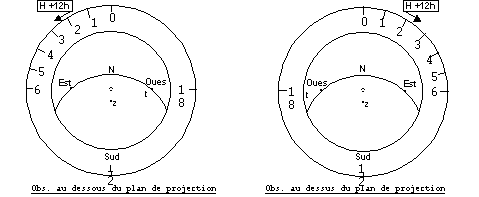
- Projection des cercles verticaux passant par Zénith
et Nadir d’un lieu à la latitude f
- Projections des cercles de hauteur (sur
l’hémisphère nord)
Soit E E’ un cercle de hauteur h
Soient e et e’ leurs projections et t le centre du cercle projeté
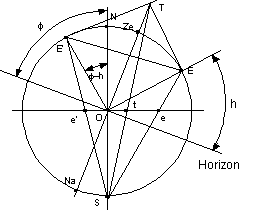
Position du centre t
Oe’= atg((f-h)/2) Oe= atg((p-f-h)/2)=acotg((f+h)/2)
Ot(h)= Oe - ee’/2 =(Oe-Oe’)/2 =a(tg(p-f-h)/2 - tg(f-h)/2)/2 = acosf/(sinh +sinf)
Rayon du cercle projeté
R(h)= (Oe+Oe’)/2=a(tg(p-f-h)/2 + tg(f-h)/2)/2 = acosh/(sinh +sinf)
Tracé du cercle horizon: h=0
Position du centre du cercle horizon: Ot(h=0)= acotgf
Rayon du cercle horizon: R(h=0)= a/sinf
h
90
80
70
60
50
40
45,0
30
20
10
0
-6
-12
-18
Ot(h)
2,07
2,09
2,15
2,25
2,40
2,62
2,50
2,93
3,37
4,01
5,00
5,87
7,08
9
R(h)
0,00
0,51
1,04
1,59
2,18
2,84
3
3,59
4,48
5,59
7,07
8,25
9,80
12
45
0,79 5
LATITUDE DU LIEU: A4 en °, B4 en rdValeur de a en C4 Maisons astrologiques I-XII
XII-XI
XI-X
X-IX
K 90 60
30
0 Rayon du cercle a/(sin(phi)*sinK) 7,07 8,16
14,14
#DIV/0! Distance au méridien a/tgK*sin(phi) 0 4,08
12,25
#DIV/0!
- Tracé des maisons astrologiques
- Chaque maison est limitée par un cercle passant
par les points Nord et Sud de l’horizon, faisant l’angle
K= -90° (I-XII), -60° (XII-XI), -30° (XI-X), 0°(X-IX)
avec le cercle méridien
- Les projections sont donc des cercles passant par n et
s, et dont les tangentes au méridien en n et s font les angles
K=-90°, -60°, -30°, 0°
- Le rayon du cercle horizon étant a/sinf, les rayons
seront a/(sinf*sinK)
- Les distances du centre au méridien
seront a/tgK*sinf
- Chaque maison est limitée par un cercle passant
par les points Nord et Sud de l’horizon, faisant l’angle
K= -90° (I-XII), -60° (XII-XI), -30° (XI-X), 0°(X-IX)
avec le cercle méridien
- Projections des cercles de hauteur
(sur l’hémisphère sud)
Soit E E’ un cercle de hauteur h
Soient e et e’ leurs projections et t le centre du cercle projeté
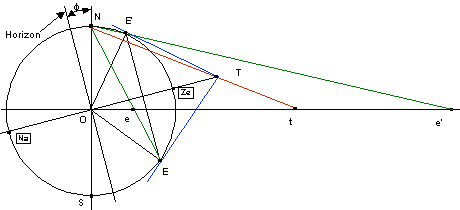
Position du centre t
Oe’= atg((p-(h-f))/2)=acotg((h-f)/2) Oe=atg((h+f)/2)
Ot(h)= Oe + ee’/2 =(Oe’+Oe)/2 =a{tg{(p-(h-f))/2} + tg{(h+f)/2}}/2 = acosf/(sinh -sinf)
Rayon du cercle projeté
R(h)= (Oe’-Oe)/2= a{tg{(p-(h-f))/2} - tg{(h+f)/2}}/2 = acosh/(sinh -sinf)
Tracé du cercle horizon: h=0
Position du centre du cercle horizon: Ot(h=0)= -acotgf
Rayon du cercle horizon: R(h=0)= a/sinf
h
90
80
70
60
50
40
30
20
14,53 10
0
-6
-12
-18
Ot(h)
6,57
6,71
7,14
8,00
9,55
12,6
19,8
54,0
0,0
-63,7
-19,6
-13,8
-10,7
-8,8
R(h)
0,00
1,18
2,48
4,06
6,24
9,77
17,4
51,6
0,69 -63,8
-19,9
-14,0
-10,7
-8,49
Oe 6,46 5,41 4,54 3,80 3,16 2,58 2,05 1,55 1,30 1,09 0,64 0,37 0,11 -0,15 14,53
0,25 5 LATITUDE DU LIEU: A4 en degrés, B4 en radians Valeur de a en C4
- Tracé des maisons astrologiques
- Tracé de l’astrolabe
(Partie mobile)
- Tracé des cercles d’égale
déclinaison (sur l’hémisphère nord)
D’après la formule III.2.: r=atg(p/4-q/2) et avec a = 5
q
80
70
60
50
45
40
30
23
20
10
0
-10
-20
-30
-40
-45
r
0,44
0,88
1,34
1,82
2,07
2,33
2,89
3,28
3,50
4,20
5
5,96
7,14
8,66
10,7
12,1
- Projections de cercles particuliers
* L’équateur se projette en lui-même
* Les tropiques sont tracés en utilisant les formules de I.5. avec
q = +e= +23°27’ (Tropique du Cancer) q = -e = -23°27’ (Tropique du Capricorne)
* L’écliptique se projette en un cercle tangent aux deux tropiques.
Son rayon est r = a/cose et Ot = atge (avec a=5, r=5,450 et Ot = 2,168)
- Projections des étoiles principales
On peut fabriquer un index appelé alidade gradué en déclinaison q de +90° à par exemple -30°. À l’aide des graduations en déclinaison q et des graduations en ascension droite a on porte sur l’araignée les étoiles souhaitées.
- Graduation du pourtour de l’araignée
* L’intersection avec l’équateur céleste donne les points g et g’. On appelle g celui qui sera pris pour origine des ascensions droites et on gradue en ascension droite a de 0 à 24H dans le sens
- rétrograde si l’observateur est à l’intérieur de la voûte céleste
- positif si l’observateur est à l’extérieur de la voûte céleste

- Graduations supplémentaires
de l’araignée
a) Temps solaire vrai Hsv=angle horaire du soleil au lieu d’observation
Le soleil parcourt à vitesse non constante l’écliptique en 365,2422... jours (soit a0 son ascension droite). On peut donc diviser le pourtour de l’araignée en 364,2422 parties inégales et graduer chaque jour de l’année en face de l’ascension droite du soleil à 0h00 T.U. ce jour. D’une année sur l’autre ces graduations se déplacent un peu (car l’équinoxe a lieu entre le 20 et le 21 mars, c’est à dire que le 21 mars à 0h00 T.U. le soleil vrai n’est pas chaque année à l’ascension droite 0h00). Le 1er janvier à 0h00 T.U. l’ascension droite du soleil est en moyenne18h43. On peut corriger le faible écart pour une année donnée avec des tables (voir carte Sirius). On doit également faire une correction de fraction de jour correspondant à l’heure d’observation. (Nous ne ferons pas ces corrections)
b) Temps solaire moyen: Hsm = Hsv + E
Le temps solaire moyen correspond au temps solaire vrai "corrigé de ses irrégularités " (angle variant linéairement en fonction du temps de la mécanique). C’est une entité échappant à l’observation directe et dont la définition suppose la connaissance préalable des mouvements de rotation et de translation de la Terre. Les valeurs du terme correctif E, terme appelé équation du temps, se lisent pour chaque jour de l’année dans des éphémérides ou sur une courbe.
On calcule E=-3mn le 1er janvier. On divise le pourtour de l’araignée en 364,2422 parties égales correspondant au temps solaire moyen et on fait coïncider la graduation du 1er janvier avec l’ascension droite 18h40.
c) On peut aussi diviser l’écliptique en 360° représentant la longitude géocentrique du soleil.
- Tracé des cercles d’égale
déclinaison (sur l’hémisphère sud)
D’après la formule III.2.: r=atg(p/4+q/2) et avec a = 5
q
80
70
60
50
45
40
30
23
20
10
0
-10
-20
-30
-40
-45
r
0,44
0,88
1,34
1,82
2,07
2,33
2,89
3,28
3,50
4,20
5
5,96
7,14
8,66
10,7
12,1
- Projections de cercles particuliers
- Utilisation de l’astrolabe
- Position du soleil moyen le ...
- Heure de lever du soleil et azimuth le ...
- Durée du jour le ...
- Durée des crépuscules
* civil (h=-6° sous l’horizon): par temps clair les planètes et les étoiles de première grandeur sont visibles
* nautique (h=-12° sous l’horizon): les étoiles de deuxième grandeur sont visibles, horizon encore discernable
* astronomique (h=-18° sous l’horizon): les étoiles de sixième grandeur sont visibles, il fait nuit
Le calcul de l’angle horaire donnerait cosH=(sinh-sinfsind)/cosfcosd h hauteur, f latitude, d déclinaison
f=45°, Équinoxes, d=0° (32mn, 1h06, 1h39), 21 juin, d=23° (39mn, 1h28, 2h34), 21déc (35mn, 1h02, 1h49)
- Jour du plus petit crépuscule
Le jour du plus petit crépuscule, la déclinaison d du soleil est donnée par par sind=sinftgh/2, h hauteur choisie sous l’horizon; on en déduit le jour puis la durée de ce crépuscule.
Problème résolu pour la première fois par Nunez (1492-1517), géomètre portugais
-
Hauteur du soleil lors du passage au méridien
le ...
- Heure
* à laquelle votre ombre est égale à votre hauteur le ...
* à laquelle votre ombre est égale à votre hauteur plus la longueur de votre ombre à midi le ...
* à laquelle Antarès culmine le ... * à laquelle se lève la lune qui se trouve à l’ascension droite ....
- Angle sous lequel le soleil
se couche
La projection conservant les angles, on peut mesurer au rapporteur l’angle écliptique-horizon au coucher du soleil
- Position du soleil moyen le ...
- Trigonométrie
sphérique
- Historique
Hipparque (vers 150 av J.C.): parait le premier inventeur de la trigonométrie sphérique (“art de trouver les parties inconnues d’un triangle tracé sur une sphère par le moyen de celles que l’on connait”)
Ménélaüs (vers 80 av J.C.): Une traduction latine des ”Sphériques” nous est parvenue mais le traité “Sur les cordes” est seulement évoquée par d’autres auteurs
Ptolémée (vers 150 ap.J.C.): laisse dans l’Almageste un traité complet de trigonométrie rectiligne et sphérique, le seul qui nous soit parvenu directement des Grecs.
Albategni (877-929): substitue la notion de sinus à celle de corde et fait connaître la formule fondamentale de trigonométrie sphérique: sina/sinA = sinb/sinB = sinc/sinC
- Relations dans un triangle
sphérique (formé d’arcs de grands
cercles de la sphère)
Triangle sphérique: dans le triangle ABC tracé sur la sphère de rayon 1, les cotés a, b, c, sont inférieurs à p
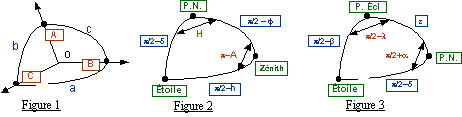
Groupe de Gauss (Figure 1)
* cosa = cosb*cosc + sinb*sinc*cosA * sina*sinB = sinb*sinA * sina*cosB = cosb*sinc - sinb*cosc*cosA
Coordonnées horizontales: hauteur h azimuth A (sud A=0°, ouest A=90°, nord A=180°, est A=270°)
Coordonnées équatoriales:
*d déclinaison et a ascension droite
*H angle horaire (repérage par rapport au méridien sud)
demi-plan vertical zénith:sud H= 0h, puis + vers l’ouest H=6h, 12h (nord),18h(est).
A azimuth
Relations entre coordonnées horizontales et équatoriales (Figure 2)
On place le zénith en B, le pôle en A, une étoile en C et les relations de Gauss deviennent
cos(p/2-h) = cos(p/2-d)cos(p/2-f) + sin(p/2-d)*sin(p/2-f)*cosH
sin(p/2-h)*sin(p-A) = sin(p/2-d)*sinH
sin(p/2-h)*cos(p-A) = cos(p/2-d)*sin(p/2-f)- sin(p/2-d)*cos(p/2-f)*cosH
sinh = sinf*sind + cosf*cosd*cosH
cosh*sinA = cosd*sinH
cosh*cosA = - cosf*sind + sinf*cosd*cosH
Relations entre coordonnées équatoriales et écliptiques (Figure 3)
On place le pôle de l’écliptique en A, le pôle céleste Nord en B, une étoile en C
cos(p/2-d) = cose*cos(p/2-b) + sin(e)*sin(p/2-b)*cos(p/2-l)
sin(p/2-d)*sin(p/2+a) = sin(p/2-l)*sinH
sin(p/2-d)*cos(p/2+a) = cos(p/2-b)*sine- sin(p/2-b)*cose*cos(p/2-l)
sind = cose * sinb + sine * cosb * sinl
cosd * cosa = cosb * cosl
cosd * sina = - sinb * sine + cosb * cose * sinl
cos(p/2-b) = cose*cos(p/2-d) + sine*sin(p/2-d)*cos(p/2+a) Š sinb = cose*sind - sine*cosd*sina
- Historique
- De l’astrolabe
à la carte du ciel
- De la projection stéréographique
de l’astrolabe à la carte du ciel
Sur l’araignée de l’astrolabe les cercles d’égale déclinaison sont donnés par la formule I.5.: r=atg(p/4-q/2). Les cercles s’élargissent considérablement à la périphérie et les constellations de l’horizon nord sont très petites par rapport à celles de l’horizon Sud. Pour remédier à cette disproportion on choisit, pour des écarts égaux en déclinaison, de faire des cercles équidistants.
- Comment tracer la ligne d’horizon
sur la carte du ciel ainsi modifiée
Les relations entre coordonnées horizontales et équatoriales deviennent pour l’intersection de l’horizon (hauteur h=0) avec la courbe de déclinaison d, à la latitude f=45°
cosH = - tgftgd= - tgd
sinA = sinHcosd et cosA = -sind/cosf= -1,414sind
- Comment graduer la ligne d’horizon
en azimuth
On inverse les formules et pour A donné
on trouve d = Arcsin(-cosA*cosf) = Arcsin(-0,707cosA) et H= Arcsin(sinA/cosd) ou cosH = - tgftgd = - tgd
- Comment tracer la ligne Est
- Zénith - Ouest:
Pour l’azimuth A= 90°, on trouve d puis H, et on fait de même pour A= 270°
Pour A=90° on trouve H= arcos (tgd/tgf)
- Figures et tableaux (Ils
sont donnés pour la latitude f=45°)
- De la projection stéréographique
de l’astrolabe à la carte du ciel
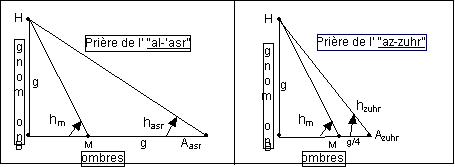
- Tracé des heures
de prières de midi et de l’après-midi (Al-Biruni)
45,0 LATITUDE DU LIEU EN A1 Déclinaison du soleil en A2 Début de la prière de l'aprés-midi d -23,5 -20,0 -10,0 0,0 10,0 20,0 23,5 hmidi (°) 21,6 25,0 35,0 45,0 55,0 65,0 68,5 hal-asr (°) 15,8 17,6 22,4 26,6 30,5 34,3 35,6 H (°) 31,4 34,9 43,7 50,8 56,5 61,1 62,3 H en heure 14,1 14,3 14,9 15,4 15,8 16,1 16,2 H (ANTI SOLAIRE) 2,1 2,3 2,9 3,4 3,8 4,1 4,2 Début de la prière de midi hal-zuhr (°) 19,8 22,7 30,8 38,7 46,5 54,4 57,2 H (°) 17,2 19,3 24,3 27,9 30,2 30,7 30,5 H en heure 13,1 13,3 13,6 13,9 14,0 14,0 14,0 H (ANTI SOLAIRE) 1,1 1,3 1,6 1,9 2,0 2,0 2,0
- hmidi = 90 - f +
d
1 - cosH = (sinhmidi - sinh)/(cosfcosd)
H = 1 - (sinhmidi-sinh)/(cosfcosd)
- Prière de l’après-midi
cotan(h )= cotan(hmidi) + 1
h = ATAN (tanhmidi/(1 + tanhmidi))
- Prière de l’après-midi
- Prière de midi
cotan(h)=cotan(hmidi) +0,25
h=ATAN(tanhmidi/(1 + 0,25*tanhmidi))
- hmidi = 90 - f +
d
- Bibliographie
- Cahiers Clairaut n ° 47 et n ° 48
- Traité de l’astrolabe Edition Alain Brieux
(épuisé) Henri Michel
- Cadrans solaires et astrolabes I.R.E.M. de Limoges, 123
Av Albert Thomas 87000 Limoges
- Astronomie, méthodes et calculs Masson A. Acker
et C Jaschek
- Astronomie générale Éditions A.
Blanchard André Danjon
- Les cadrans solaires Éditions Oberlin René
R.J. Rohr
- L’astrolabe Association Française de Topographie Raymond d’Hollander
- Cahiers Clairaut n ° 47 et n ° 48
- Tracé des cercles d’égale
déclinaison (sur l’hémisphère nord)
I.U.F.M. de Lyon Page #/#