Repérage Espace et Temps
I) Rotation, révolution et précession...
II) Mouvement de la Terre sur lécliptique..
Les débuts du repérage en mer..
I) Les premiers outils du navigateur..
II) Méthodes astronomiques de détermination des longitudes.
Histoire de la mesure du temps.
II) Débuts de lhorlogerie mécanique..
III) Quelques grands noms de la mesure du temps.
I) Le problème de la latitude..
X) Méthode des droites de hauteur..
II) Musées en France et en Europe..
Homme libre, toujours tu chériras la mer !
La mer est ton miroir ; tu contemples ton âme
Dans le déroulement infini de sa lame,
Et ton esprit nest pas un gouffre moins amer.
Les Fleurs du mal, Charles Baudelaire

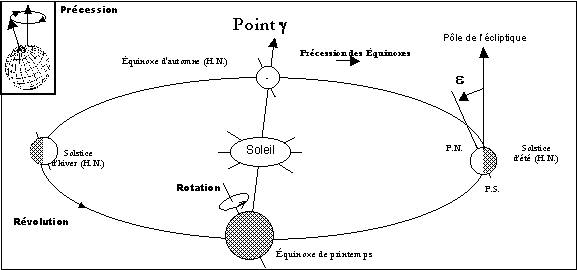
Document 1: Mouvements de la Terre
Dans un premier temps on considèrera que la terre est animée uniquement des mouvements de
· rotation autour dun axe appelé axe des pôles, de durée « jour » (précisions plus loin)
· révolution autour du soleil dans un plan (plan de lécliptique) dont la normale est inclinée dun angle e (obliquité) par rapport à laxe des pôles : la durée de cette révolution est denviron 365jours 5h 48mn
· précession : laxe de rotation subit une révolution en 26 000 ans autour du pôle de lécliptique
La position du soleil à linstant de léquinoxe de printemps définit le point g accessible seulement indirectement à lobservateur. Printemps, été, automne, hiver feront référence à lhémisphère nord
Par suite du mouvement de précession de la Terre, g nest pas fixe
Le mouvement de nutation non considéré ici correspond à la variation (faible) de lobliquité e ci-dessus
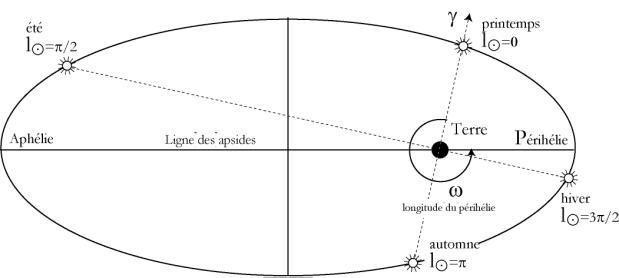
Les équations sont inchangées si on considère le mouvement (apparent) elliptique du soleil autour de la Terre Éléments moyens du mouvement (BDL), t mesuré en milliers d'années juliennes à partir de J2000
· Longitude du périhélie w =282,937° + 61 900".552t + nous prendrons w =283°
· a demi-grand axe a=1,000 001 0178
· e=c/a lexcentricité e=0,016 708 6342 0,000 420 3654t +
· b demi-petit axe c=b/a demi-distance entre foyers
Les planètes décrivent une courbe plane qui est une ellipse dont le soleil occupe un des foyers
Le rayon vecteur Soleil-Planète décrit une aire proportionnelle au temps (Loi des aires)
Les carrés des temps des révolutions T de deux planètes quelconques sont dans le même rapport que les cubes de leurs demi-grand axes a: T2/a3 = Cte
v anomalie vraie : angle entre le rayon vecteur TS et TP
u : anomalie excentrique : on utilise le cercle de rayon a inscrit dans lellipse
l€= w +v : longitude du soleil à linstant t
Lellipse (demi-axes a et b) est la projection du cercle ayant pivoté de langle a autour du grand axe tel que cosa=b/a
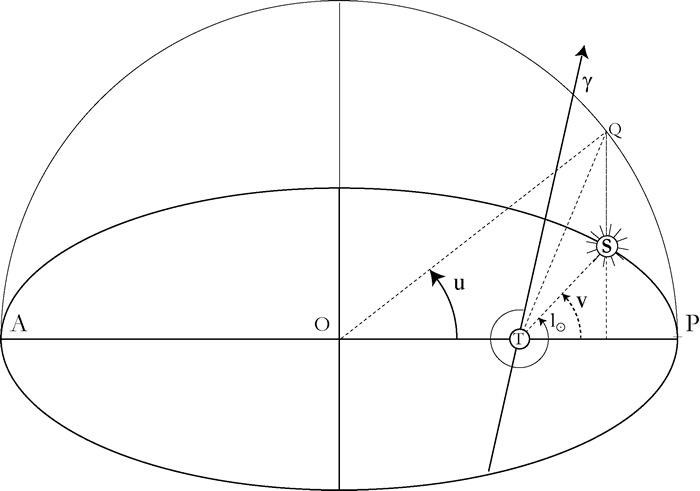
Lellipse étudiée est la projection du cercle définit ci-dessus et lairePTS cherchée est la projection de lairePTQ donc AirePTS=AirePTQ*b/a (la projection a pour cosinus b/a)
Or AirePTQ= Aire secteur circulaireOPQ - Aire Triangle OTQ=(a2*u - c*asinu)/2=a2(u-e*sinu)/2
soit T la durée de révolution, soit t0 linstant de passage au périgée, la 2ième loi exprime que les aires décrites par le rayon vecteur croissent proportionnellement au temps : Aire PTS=pab(t-t0)/T
Finalement pab(t-t0)/T=ab(u-esinu)/2 soit
u-e*sinu=2p(t-t0)/T=n(t-t0)=M Équation de Képler
n, appelé moyen mouvement, représente la vitesse angulaire moyenne
M=n(t-t0) représente la valeur que prendrait lanomalie u si le mouvement était uniforme
x=rcosv=a(cosu-e)
![]()
x2+y2=r2 donc a2(1-ecosu)2=r2
et![]() doù
doù ![]() équation de
lellipse en coordonnées polaires
équation de
lellipse en coordonnées polaires
r(1+cosv)=a(1-e)(1+cosu)
r(1-cosv)=a(1+e)(1-cosu)
![]()
On se donne une unité de temps pour exprimer la période T doù M
On résout léquation de Képler, on trouve u(t), on en déduit v(t) puis r(t)
x=acosu=rcosv+ae et![]() doù
doù ![]() et
et![]()
on en déduit ![]() =esinu +
au
1er ordre
=esinu +
au
1er ordre
or u=M+esinu donc v=M+2esinu + et r=a(1-ecosM + )
l€= w +v = w +M+2esinM +
la longitude du soleil comprend le terme M qui croit linéairement en fonction du temps et un terme 2esinM (donc de période T car si t croit de T, M croit de 2p) appelée équation du centre C
Lamplitude de cette inégalité vaut 2e=2*0,01673rd=115 presque 2° . Les babyloniens, Hipparque et bien sûr Ptolémée connaissaient cette inégalité. Pour lexpliquer Ptolémée adjoignait au cercle déférent parcouru par le soleil un épicycle
l€=
w +v = w
Pour les navigations en Méditerranée aucune connaissance astronomique nétait nécessaire et il ny eut jamais de navigation astronomique. Des livres étaient néanmoins utiles aux marins, les portulans (portolano, pilote en italien au départ journal de bord du pilote) puis livres portulan au 12ième siècle (informations sur les côtes et les ports, les courants) puis advinrent les cartes-portulans accompagnant le livre. Lexpédition de Saint Louis à Tunis mentionne lusage dune telle carte
La plus ancienne carte de la Méditerranée bien différente des cartes monastiques la « carte pisane » date de cette époque.
1569 : carte de Mercator : projection cylindrique conforme (respecte les angles.
La boussole viendrait des chinois et aurait servi à la géomancie dès le 1er siècle après J.C.: on faisait tourner une cuillère taillée dans de la magnétite sur une plaque de bronze et on regardait dans quelle direction elle sarrêtait.
Des textes[1]de 1250 parlent de la « Marinette » ce qui indique que les marins sen servaient dès le début du 13ième siècle voir du 12ième siècle en Europe.
On lappelait aussi parfois « calamite » (latin calamus = roseau), parce quon enfilait une aiguille dans un roseau flottant sur leau. Elle se modernise rapidement pour être solidaire dune rose des vents avec au départ 8 rhums (ou rhumbs = vents), les 8 vents de Méditerranée puis16 voir parfois 32.
La variation de la déclinaison en fonction du lieu est notée par Christophe Colomb dans son journal de bord
http://www.cristobal-colon.net/documentation/C07p7.htm
Edmund Halley trace des cartes de déclinaison magnétique vers 1700. Les courbes dégale déclinaison (isogones) avec une mise à jour régulière, permettent en théorie de se repérer en longitude : la méthode est néanmoins peu précise, nest valable que si les isogones sont à peu près parallèles aux méridiens, là où elles sont régulières et ne changent pas trop rapidement. De plus la déclinaison est difficile à mesurer avec une grande précision..
Linclinaison magnétique nest connue que vers 1550
De 1415 à 1460, avec leur roi Henri le Navigateur, les Portugais (École Royale de Sagres) explorent les côtes de lAfrique : les instruments dastronomie utilisés à terre apparaissent alors sur les bateaux pour mesurer la latitude : quadrant et astrolabe nautique puis arbalestrille. La navigation à « lestime » fait place à la navigation de latitude ou hauturière (de haute mer). On tient aussi compte de lécart de la Polaire par rapport au pôle céleste Nord.
Pedro de Medina, instructeur royal d'Espagne, explique dans un ouvrage célèbre "Arte de navigar" comment calculer sa latitude à partir de la hauteur méridienne du soleil ou de la hauteur de l'étoile polaire.
Le traité de Tordesillas de juin 1494 précise la ligne de marcation (ouest pour les Espagnols, est pour les Portugais) entre les terres appartenant aux rois catholiques, Ferdinand dEspagne et Jean du Portugal: dabord 100 lieues puis 370 lieues à lOuest des îles du Cap vert et non à X degrés de longitude).
On comprend limportance du loch apparu vers les années 1450 : connaissant la direction prise grâce à la boussole et la vitesse du navire par rapport à leau, on peut connaître de façon approximative son déplacement (en négligeant les courants marins ). Le loch sera utilisé du 15ème à la fin du 17ème pour estimer la position du navire ; il lest encore pour estimer sa vitesse par rapport à leau
Dans sa première version (log = bûche en hollandais), on aurait simplement jeté la "bûche" à lavant du navire et compté en combien de temps il atteignait lextrémité.
Par la suite le loch était composé dun flotteur en forme de triangle sphérique équilatéral lesté à deux des angles et muni de trois cordes réunies à la ligne de loch.
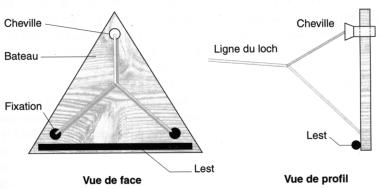
Enroulée sur un touret la ligne de loch porte différentes marques. La première, la houache, est un morceau détoffe fixée à 1 longueur de ligne égale à la longueur du navire. Les divisions appelées nuds se succèdent de ½ nud en 1/2 nud. Quand la houache passe, on retourne un sablier de 30 secondes. Quand celui-ci est vide on rentre le loch à bord en comptant le nombre de nuds (précision acceptable pour des vitesses inférieures à 15 nuds). La distance entre deux nuds étant de 1/120 mille marin, le nombre de nuds comptés en 30s donne exactement la vitesse du navire en mille marin à lheure : Ainsi 15 nuds donne 15 mille à lheure soit environ 28km/heure
1 mille marin : 1 de longitude au niveau de léquateur terrestre = 2*p*6 371 / (360*60) =1 853,2 m
1 nud théorique : 1/120 mille marin : 15,44 m
1 lieue marine = 3 milles = 5556m = 3 de longitude
Le loch nétant pas immobile par rapport à leau mais étant entraîné un peu par le navire, la distance entre les nuds de la ligne de loch, appelée nud pratique nest que de 14,50 m
On mesure les heures solaires locales dobservation dun phénomène astronomique en deux lieux et on les compare
Cest une idée suggérée par les astronomes de lAntiquité, Hipparque notamment.
On peut prévoir quand on va opérer (les babyloniens connaissaient déjà les cycles des éclipses de lune) mais la précision est modeste car les bords de lombre de la Terre sur la lune est assez floue)
Pline lAncien (né en 23 à Côme, mort en 79 lors de l'éruption du Vésuve , Histoires Naturelle, Livre II chapitre 70 raconte : « A Arbéles, lors de la victoire dAlexandre le Grand, la lune séclipsa, selon la tradition, à la 2e heure de la nuit, tandis quen Sicile, ce phénomène eut lieu à son lever ».
On en déduit quentre Arbéles (Assyrie) et le lieu dobservation en Sicile il y a environ 2*15=30° de longitude (en fait 27°). Cette éclipse eut lieu le 21 septembre 332
Ptolémée (Géographie I, chapitre 4) cite une éclipse observée en 70 après J.C. qui se produisit à la 5ième heure de la nuit à Arbéla et à la 2ième heure de la nuit à Carthage.
Les observations comparées de Peiresc à Marseille et dun ami en Syrie, lors de léclipse de lune du 27 août 1635, permettent de raccourcir la longueur estimée de la Méditerranée de 1 000 km
En 1685 J.D. Cassini I et Philippe de la Hire trouvent la longitude de Québec en observant une éclipse de lune en même temps que Deshaye au Canada
Ce sont les passages de Vénus devant le soleil qui sont assez rares
Le transit du 3 juin 1769 permet à deux astronomes américains(Ewing et Prior) de mesurer la longitude de Philadelphie par rapport à Paris.
Vers 1611, juste après la découverte des satellites de Jupiter par Galilée (grâce à sa lunette) on put déterminer la longitude exacte de Malte en observant les éclipses des satellites de Jupiter, à Malte et Marseille
Römer en 1675, en observant les éclipses des satellites, découvre quelles nont pas lieu avec la régularité prévue : par rapport aux mesures faites lorsque Jupiter et la Terre sont en quadrature, les éclipses avancent de 9mn lors dune conjonction T-J, retardent de 9mn lors dune opposition T-J. Il en déduit que la propagation de la lumière nest pas instantanée et peut établir des tables précises.
En 1703 et 1704, J. D. Cassini II trouve la longitude de Port au Prince en observant les éclipses des satellites en même temps que le Père des Minimes, Louis Feuillée à la Martinique
Vers 1715 la précision est de ½ degré (Newton avance même ¼ degré)
La lune se déplace le plus rapidement de tous les astres (33 " en moyenne en 1 minute de temps) = aiguilles dune horloge dont le cadran est la voûte céleste et les points du cadran sont les étoiles.
On compare lheure locale de passage de la lune (par exemple à 30° de létoile Régulus) à lheure locale de Greenwich de ce même événement, heure donnée par des tables.
Une erreur de 1 sur la lune donne une erreur de 2mn de temps soit 0,5° de longitude
· Moyen dobserver et de mesurer les distances angulaires avec précision
· Méthodes de calcul pour éliminer la parallaxe et la réfraction de la mesure (il fallait 4 heures de calculs pour trouver la longitude vers 1700)
· Pendant 12 jours autour de la Pleine Lune où on ne peut mesurer directement son angle avec le soleil, trop important, il faut utiliser une montre précise gardant lheure solaire du lieu pendant 18h pour en déduire cet angle.
· Tables journalières donnant distances lunaires en un lieu de référence donné
La méthode est inutilisable 6 jours autour de la Nouvelle Lune où la lune est invisible
Ptolémée vers 180 après J.C., consacre un chapitre à la variation de durée du jour solaire (mouvement non constant du soleil sur lécliptique connu depuis les Babyloniens) et donne une table de léquation du temps
De nombreuses Tables furent élaborées avant les suivantes, les plus connues
Tables de Tolède (1080) dal-Zarquali et Ibn Saïd de Cordoue
Tables Alphonsines (1252) : sous Alphonse X, Roi de Castille et de Léon (1221-1284) : 16 livres diffusés dans toute lEurope : une centaine de manuscrits puis des milliers dexemplaires imprimés : utilisés jusque vers 1600. Elles comportent des tables de déclinaison du soleil permettant de trouver la latitude en mesurant la hauteur du soleil à midi avec une précision de 1° à 2°, ainsi que les coordonnées des planètes
Tables Pruténiques de Reinhold en 1551 : équation du temps et coordonnées des planètes avec les hypothèses de Copernic (avec des trajectoires circulaires pour la Terre et les planètes )
Tables Rudolphines publiées en 1627 par Kepler (avec des trajectoires elliptiques pour les planètes)
Tables de Newton vers 1713 : 5 sur la lune
Les tables déquation du temps sont appelées équations des horloges au 17ème et 18ème siècle
1730 Grandjean de Fouchy trace la courbe en 8 des cadrans solaires à partir des tables de Flamsteed
Tables de Tobias Mayer de la position de la lune en 1754 (avec équations dEuler) : 1,5 sur la lune
Tables de Damoiseau (1824) puis Hansen (1857) basées sur théorie de Laplace : 1 sur la lune
Almanach nautique et éphémérides astronomiques (de 1766 à 1907) : position de la lune toutes les 3h
· - 3500: Clepsydres (qui vole leau)
· - 1500: Cadrans solaires: Incas, Égyptiens, Grecs, Hindous, Chinois, Romains
· + 700: Sablier (le verre est connu depuis 1500 mais il est difficile de réaliser une double fiole étanche maintenant le sable sec). Vers 1300, le sablier se développe (navires, palais de justice, églises, écoles...) et sera très employé jusquen 1780, en navigation en particulier
· Horloges à eau : différents mécanismes furent utilisés au cours des âges pour que lécoulement de leau se transforme en mouvement dindex voir daiguille sur un cadran. Certaines sont restées célèbres.
F Vers 480 Platon équipe une clepsydre, dune chambre munie dun sifflet ; la pression augmentant, le sifflet peut jouer son rôle de réveil
F La Tour des vents, Tour octogonale construite vers 75 avant J.C., toujours visible à Athènes avec ses cadrans solaires, abritait une horloge à eau aujourdhui disparue
F Vitruve, architecte de Jules César, décrit dans « de architectura » lhorloge de Ctésibios (vers 150 avant J.C.) (reconstitution au musée de Wuppertal)
F En 757: le pape Paul 1er offre une horloge à eau au roi Pépin le Bref
F En 1092 une horloge à eau monumentale, à rouages (inventés vers 1400 en Europe), fut construite par le chinois Su Sung. Cest la première machine à échappement. Une roue à godet entraînait au sommet dune tour de 10m, une sphère armillaire donnant la position réelle des étoiles (reconstitution au Science Museum de Londres)
· Heure de Nuremberg : 2 fois 12 heures : du lever au coucher et coucher au lever
· Heure « empire germanique » : 2 fois 12 heures jour comptées à partir de minuit
· Heure gauloise : 2 fois 12 heures jour comptées à partir de midi
· Vers 1300 : heure égale de 60 minutes et jour divisé en 24h
F Heure italienne : 24 heures commençant au coucher du soleil
F Heure tchèque : 24 heures commençant (1/2 heure après le coucher)
F Heure babylonique : 24 heures commençant au lever du soleil
Horloges monastiques pour sonner les heures canoniales (prévues par « les canons de lÉglise) » fixées à sept par saint Benoît (480-550).
Vers 1250 : horloges à poids, à verge, foliot et roue de rencontre (mécanisme régulant la descente du poids) : inventé en Italie par un obscur génie : précision de 30mn/jour : 2*10-2
À partir de 1300, il y a des horloges sur les tours des églises puis dans toutes les grandes villes. Elles ont une seule aiguille et sont remises à lheure à midi à laide du cadran solaire
Vers 1400 : premières horloges à ressort spiral moteur (le principe était connu mais les ressorts sont difficiles à fabriquer, à courte duré de vie, le fer est cassant). La tension du ressort est régulée par une fusée ou une came, le stackfreed ; « loscillateur » est le foliot. On peut alors fabriquer de petites horloges domestiques.
Vers 1500 : premières montres en Allemagne, Hollande et France
1518 François 1er achète deux coûteuses montres de poche à Jean Couldray de Blois, horloger
1583 : Galilée à Pise découvre lisochronisme des petites oscillations, Santorio imagine un procédé pour compter les oscillations
Richelieu fait admirer ses montres et en fait tomber deux. « Cest la première fois quelles vont ensemble »
1657 : Christiaan Huygens trouve le moyen dentretenir le balancier par le poids lui-même: première horloge à pendule (fabriquée par Salomon Coster); cest la période propre du balancier qui impose le rythme
1671 : William Clément ancien fabricant dancre devenu horloger fabrique daprès une idée de Robert Hooke « lancre à recul » : permet une oscillation dun angle de 3 à 4° du pendule au lieu de 40° dans lhorloge de Huygens et de bien réaliser lisochronisme
1676 : Christiaan Huygens fait réaliser par lhorloger Isaac Thuret une montre à ressort spiral réglant
Les montres et horloges peuvent désormais posséder une aiguille des heures et une aiguille des minutes
Deux sources derreur passent maintenant au premier plan
· variation de température
pendule à grill bimétallique de Harrison, à mercure de Graham
raquette bi-lame ou châssis bi-métallique pour les montres
· friction
F aux points dengrènement : forme épicycloïdale des dents (Desargues, Römer, La Hire en 1694) ; machines à tailler les roues dès 1700
F aux pivots : rubis dès 1704 : montre à 17 rubis
F à léchappement : échappements à repos et échappements libres
1715 : George Graham et son élève Thomas Tompion : « échappement à repos sans recul » le mécanisme qui entretien les oscillations nen perturbe pas la période puis échappement à cylindre (1725)
1754 : échappement libre à « ancre continentale » de Mudge : résistant aux mouvements brusques donc idéal pour une montre
1811: adoption de lheure solaire moyenne de Greenwich pour lheure légale en Angleterre
1840: 1ère horloge électrique de von Steinheil et Bain : une tension électrique fournit lénergie à loscillateur. En 1867, à lexposition universelle de Paris, elles sont une révélation (accumulateurs dans le socle)
1880 : installation dans les rues, avec léclairage, dhorloges actionnées par le courant de la ville
1870: la montre se démocratise : montre à 1$ aux U.S.A.
1891: adoption de lheure solaire moyenne de Paris pour lheure légale en France (en pratique depuis 1850 avec les chemins de fer)
1895: Conférence Internationale de Washington: création de 24 fuseaux horaires; la France vote contre, garde lheure de Paris, et ne salignera sur Greenwich quen 1911 en retardant son heure légale de 9mn 21s
1900 : construction de la plus précise des horloges à balancier (compensation
en Température, pression) 10-7
1928: première horloge à cristal de quartz de W.A. Marrison (dimensions 3m*2,5*1m):
la fréquence du quartz est lié à ses dimensions et dépend peu des conditions
extérieures et la précision est de 10-8
1933 : Mise en service de lhorloge parlante de Paris (aujourdhui au téléphone: 36 99)
1968 : première montre à quartz bon marché : Seiko (vibre à 32 768 = 2+15 Hz pour 1/100mm dépaisseur, le circuit électronique divise 15 fois par deux pour envoyer une impulsion 1 fois/s)
1955 : 1ère horloge atomique, oscillateur à molécule damoniac NH3, 1967 : étalon de césium 10ns/jour 10-13
1984 : première fontaine atomique (horloge atomique avec refroidissement des atomes) : précision 10-14
2000 : fontaine atomique 0,01ns/jour = 10-16
1400 : 60mn/jour
1400 à 1657 : 15mn à 60mn par jour
1657 et 1676 : le pendule des horloges ou le ressort spiral réglant des montres ajoutés à l'échappement à ancre font passer l'exactitude de 15mn à 15 s /jour. L'aiguille des minutes (1675) puis celle des secondes (1690) peuvent être ajoutées, mais les montres sont encore inaptes à la navigation
1762 : montre marine de John Harrison H4: 0,1s/jour en mer
1770: montres à fractions de secondes
· Jusqu'en 1780 ce sont les cadrans solaires qui donnent l'heure et permettent de corriger les montres: l'équation du temps E est d'ailleurs appelée "équation des horloges": c'est le terme à ajouter au cadran pour régler sa montre. Les "horloges à équation" étaient destinées à convertir au temps solaire vrai le temps solaire moyen donné par les pendules
· Vers 1780 les horloges sont suffisamment précises pour être réglées sur le Temps moyen de la Capitale : Genève en 1780, Londres en 1792, Paris en 1816
· En 1811 l'heure légale en Angleterre devient
l'heure solaire moyenne de Greenwich
En 1891 l'heure légale en France devient l'heure solaire moyenne de Paris (auparavant
heure du département= heure solaire moyenne de la préfecture)
· En 1895 la conférence Internationale de Washington décide la création de 24 fuseaux horaires, de prendre le méridien de Greenwich comme méridien de référence et milieu du fuseau 0
né en 1564 à Pise, mort à Arcetri près de Florence en 1642. Il est lauteur de nombreuses découvertes en physique, notamment lisochronisme des oscillations du pendule. On dit quil fit sa découverte à 18 ans en observant le mouvement oscillatoire de la grosse lampe de bronze suspendue au sommet de la coupole de la cathédrale de Pise et en se servant pour mesurer le temps des pulsations de son pouls
né et mort à La Haye (1629-1695): mathématicien et physicien hollandais
Il introduit le pendule pour régulariser le mouvement des horloges et le ressort
spiral celui des montres. Il expose le résultat de ses recherches dans « horologium
oscillatorium » paru en 1673. Il y résout notamment le problème des courbes
tautochrones pour la pesanteur et montre à laide du calcul infinitésimal que
le pendule cycloïdal est isochrone (« tautos » même et « chronos »
temps : une balle lancée de nimporte quel point de la courbe, mue par
la seule force de la gravitation, atteint le bas de la courbe dans le même temps).
Christophe Colomb part le 3 août 1492 du port espagnol de Palos, touche les îles des Antilles (Bahamas, Cuba, Haïti) le 11 octobre et rentre le 15 mars 1493 à Palos. Dans son journal de bord de septembre il note la variation de déclinaison magnétique.
Le 8 juillet 1497, Vasco de Gama et 170 hommes partent de Lisbonne, 55 rentrent en septembre 1499
Amerigo Vespucci en 1501 descend jusquà 40° Sud, le long des côtes de lAmérique
Fernão de Magalhães quitte Séville le 10 août 1519 avec 270 hommes et 5 caravelles. 1 seule rentre au port avec 18 marins en 1522.
Philippe III dEspagne offre en 1598 (10 000 ducats) pour « le découvreur de la longitude »
22 octobre 1707 : 5 navires anglais reviennent victorieux des flottes françaises en Méditerranée. 4 navires coulent sur les récifs avec 2000 marins au large des Iles Scilly, alors que lamiral pensait être au large dOuessant
Grand Prix du Parlement anglais de 20 000 livres pour 0,5° (10 000 livres pour 1°) sur la détermination de la longitude (Acte de la reine Anne). La méthode doit être testée sur un navire à destination dun port quelconque des « Indes Occidentales » choisi par les commissaires. Si le voyage dure 6 semaines (traditionnel vers les Antilles) cela impose au plus 3s/jour. 30 de longitude à léquateur correspond à 30 milles soit environ 60 km (30 km à la latitude de Londres, distance permettant de reconnaître les côtes par temps clair)
Le Régent (France) offre en 1716 la somme 100 000 livres pour résoudre le problème des longitudes
1736 : John Harrison sembarque avec H1 sur le navire H.M.S. Centurion vers Lisbonne. Le voyage aller dure une semaine, le retour 1 mois en raison de tempêtes. A larrivée le Commandant pense voir le Start Point près de Dorthsmouth. Harrison pense être au Cap Lizard à 60 milles à louest et il avait raison. La montre H1 est une merveille de 36kg avec des roues en bois de différentes essences pour sauto-lubrifier
Septembre 1741 : H.M.S. Centurion (sans lhorloge) et 5 navires font route vers le Pacifique sud ; le 7 mars 1741 ils sengagent dans les détroits « Le Maire » malgré le scorbut qui commence à bord. 58 jours de tempête pendant lesquels on maintient cap à louest sur le // 60° Sud. Puis cap au nord à la recherche de lîle de Juan Fernandez par 35° de latitude sud. Le 24 mai il se trouve sur le 35° sud mais où ? Le navire se dirige pendant 4 jours vers louest sans succès puis deux vers lest mais ce sont les côtes arides de Patagonie. Arrivée le 7 juin sur lîle il restait 250 marins sur 500
Montre H4 (<1,5kg): William Harrison, son fils, part de Portsmouth le 2 novembre 1761, arrivée à Port Royal à la Jamaïque le 19 janvier 1762, 1 semaine après départ de Port Royal pour arriver le 26 mars : 5s après 81 jours de voyage puis ? sur lAR bien inférieur à 2mn donnant un écart de 0,5° en longitude
On met en doute la mesure astronomique de lheure à La Jamaïque et William Harrison sembarque pour un second essai : départ en mars de Portsmouth, arrivée le 15 mai 1764 à BridgeTown, à La Barbade, retour en juillet: 15s sur 156 jours. Il reçoit son prix en 1773 sur intervention du roi Georges
Le capitaine James Cook, vers 1770, emporte une réplique de H4 dans ses voyages (« notre guide infaillible, la montre ») et établit des cartes précises du Pacifique
Les Français déploient les mêmes efforts que les Anglais. En 1763 et 1766 Ferdinand Berthoud, Horloger du Roy, se rend à Londres pour voir Harrison et sa montre
En 1767, sa montre marine est testée avec succès dans un voyage vers les Canaries par J. D. Cassini IV
1000 : Rayy près de Téhéran : quadrant de 20 m de rayon : 1° (35cm) : divisé en 360 parties de 10 "
1260 : Maragha (nord ouest de lIran) : règle parallactique de 7m de rayon, mesure des hauteurs à 1' près
1424 : Samarkand (Ouzbékistan): Ulugh Beg fait construire un quadrant méridien de 40m de rayon ; le marbre est gravé tous les 0,4mm permettant une mesure de 2" darc. On mesure la hauteur dun astre ainsi que linstant du passage au méridien avec des clepsydres réglées tous les jours à midi solaire corrigé de léquation du temps. Une règle parallactique graduée en ° et ' est placée sur le toit
1530 : Collège Royal crée par François 1er
1561 : Observatoire de Kassel
1580 : Uraniborg (château du ciel), sur lîle de Hveen, crée par Tycho Brahé grâce à laide du roi du Danemark Frédéric II
1632 : observatoire de Leyde (Pays Bas)
 1667 :
Colbert achète le terrain de lObservatoire de Paris et fonde lAcadémie Royale
des Sciences
1667 :
Colbert achète le terrain de lObservatoire de Paris et fonde lAcadémie Royale
des Sciences
1675 : Fondation de lObservatoire de Greenwich
Quadrant (quart de cercle) permet de mesurer la hauteur d'un astre (3m de rayon pour celui de Tycho Brahé, avec lunette après Galilée)
Document 2: Quadrant (utilisé à Terre)
Dioptre dArchimède (viseur fixe et cylindre mobile)
Dioptre dHipparque : tige de « 4 coudées de longueur » munie dun viseur fixe à 1 fente, curseur mobile à 2 petits trous superposés permettant de mesurer le diamètre apparent dun astre (soleil ou lune). Ptolémée trouve cette dioptre meilleure que la clepsydre
 Triquetrum : Ptolémée et Copernic :
3 règles articulées
Triquetrum : Ptolémée et Copernic :
3 règles articulées
Vers 1342 : Arbalète, arbalestrille ou bâton de Jacob inventé par un juif catalan Levi ben Jarsen
Elle est constituée dune longue tige (de 1m à 1,30 m) munie de 1 à 4 marteaux perpendiculaires. La tige est graduée sur ses faces avec 1 échelle pour chaque marteau.
La visée directe était possible mais pour la hauteur du soleil, lobservateur,
dos au soleil, visait le long de la tige du côté du grand marteau et approchait
le petit marteau pour quil reçoive lombre du grand. Cette méthode ne nécessitait
quune visée sur lhorizon.
indépendance des mouvements du navire : il ny a quune seule ligne
de visée
horizon artificiel en cas de brouillard à lhorizon
1742 : Rapidement loctant devient sextant avec un arc de mesure qui passe de 90° à 120° puis sy ajoute une lunette et un vernier
Document 5: Loctant
Les calculs de latitude et de longitude furent distincts jusquen 1837, époque où fut trouvée par hasard la méthode des droites de hauteur (Sumner, capitaine de la marine marchande américaine ; méthode théorisée par lamiral Français Marc de Saint Hilaire)
En 1926 on adjoignit au sextant la crémaillère/vis tangente et le tambour
Hipparque : 1200=1/3 ° pour les étoiles ; 36 au lieu de 51/an pour la précession
Observations utilisées par Copernic : 10
Tycho-Brahé : 60 pour les étoiles principales ; il perçoit limportance de la réfraction, calculée par Hooke vers 1660 ; 25" pour certaines mesures avec son cadran mural
Flamsteed : 10 grâce à sa lunette méridienne, jusqu'à 2"
Bessel: 0,7" avec un cercle méridien
Simms avec télescope
0,1
Satelitte Hipparcos 120000 étoiles à 0,002)
Document 6: Lunette Méridienne
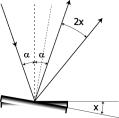 Réflexion
sur un miroir : langle a de réflexion est égal à langle a dincidence
Réflexion
sur un miroir : langle a de réflexion est égal à langle a dincidence
Si le miroir (pivotant sur un axe perpendiculaire au plan dincidence) tourne de x, le rayon réfléchi tourne de 2x
Document 7: Réflexion sur un miroir tournant
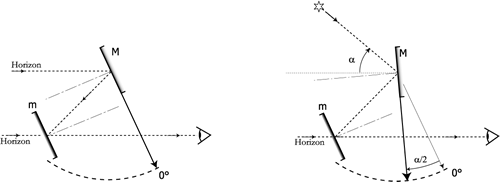
Document 8: Principe du sextant
Lorsque lalidade indique le 0° du limbe, les deux miroirs sont parallèles, limage directe et limage réfléchie de lhorizon sont confondues (première loi de la réflexion)
La deuxième loi de la réflexion montre que, lalidade ayant pivoté de langle a/2, si on vise toujours lhorizon, alors le rayon incident provient dun astre à la hauteur a
Donc sur un sextant le limbe porte un secteur angulaire de 60° qui est gradué de 0° à 120°
Dans le triangle la somme des angles est égale à 180°
Dans le triangle mMD : i + b + (180 I) =180 donc b = I - i
Dans le triangle mMA : 2i + a + (180 2*I) =180 donc a = 2*I 2*i=2(I-i) doù a = 2b
Laxe de rotation de lalidade doit passer par le centre du secteur gradué du limbe
Laxe de la lunette de visée doit être bien parallèle au plan du limbe
Les deux miroirs doivent être bien perpendiculaires au plan du limbe
Lorsque lalidade indique 0°, les deux miroirs doivent être bien parallèles entre eux : on sassure que limage directe et limage réfléchie de lhorizon coïncident (il subsiste toujours une erreur faible e de quelques minutes, que lon peut mesurer et dont on tiendra compte)
La valeur lue est notée pour le soleil Hi : hauteur instrumentale du bord inférieur du soleil
Correction de parallélisme du sextant ± e
Correction due à l'élévation de l'il (dépression apparente) -da
Correction de réfraction astronomique -R
Correction de parallaxe (dépend de la distance de lastre et de sa hauteur) +p
Correction du demi-diamètre (Soleil, Lune , Vénus) +d
Après ces corrections on obtient donc la hauteur vraie du centre du soleil
HV
HV = Hi ± e
- da R + p + d
Contrainte : visées opérées à des instants précis de la journée
 Avantage :
peu de calculs
Avantage :
peu de calculs
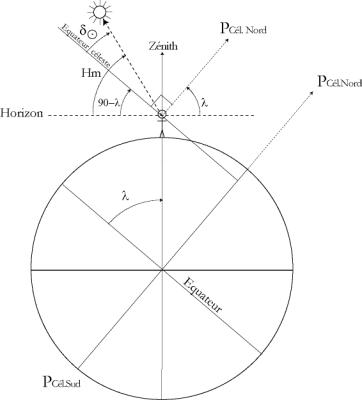
On mesure la hauteur du soleil un peu avant et un peu après sa culmination : on extrapole pour trouver sa hauteur méridienne : On connaît donc Hm
Le jour étant donné, on connaît la déclinaison du soleil d€
Le dessin montre la relation
Hm= (90 - l) + d€ on en déduit l
Utilité : sachant que la Barbade est à 16° Nord, il suffit de demeurer sur ce // et de « tracer à lOuest », poussé par lalizé pour lapercevoir un beau jour à lavant du navire
Document 9: Latitude à la méridienne
On connaît la déclinaison d de létoile et
Le sextant reste calé sur la hauteur de culmination du soleil pendant plusieurs minutes et on ne peut pas faire un Top chrono de cet instant. Deux visées sont donc nécessaires ainsi quune montre réglée en heure T.U.
· 1ère visée avant culmination
· 2ème visée après culmination lorsque le soleil se trouve à la même hauteur
On interpole pour trouver lheure T.U. de culmination doù la longitude. Il vaut mieux connaître sa longitude locale approximative ce qui permet de connaître à peu près lheure de la 2ième mesure.
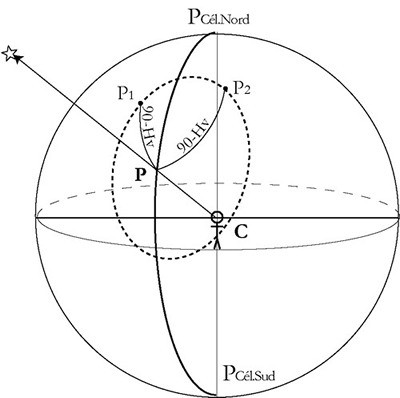
Pour un astre donné, à un instant donné, il y a un point P de la surface de la Terre pour lequel on observe cet astre au zénith : Hvraie= Hv=90°
· Hv= hauteur mesurée corrigée de lerreur instrumentale, la réfraction, la parallaxe, la dépression apparente, le demi-diamètre
Document 10 : Horizon visuel, apparent et vrai
Tous les observateurs (P1, P2, ) qui observent cet astre, au même moment, à la même hauteur Hv, se trouvent sur un cercle de centre P et de rayon 90° - Hv (exprimé en degré par rapport à laxe CP). En exprimant cet angle en minutes, on obtient la distance au point P en milles nautiques (1 mille =1 darc)
Ce cercle sur lequel se trouve lobservateur est appelé cercle de hauteur. Pour Hv=40° le rayon vaut 50° soit 3000 milles nautiques
La visée de deux astres donnent deux cercles dont lintersection donne le(s) point où lon se trouve
Cette intersection peut se trouver avec les formules de trigonométrie sphérique (il fallait plusieurs jours de calculs puis seulement 3 heures grâce aux logarithmes). Vers 1840 a été trouvée la méthode dite des droites de hauteur
Document 11: Le cercle de hauteur
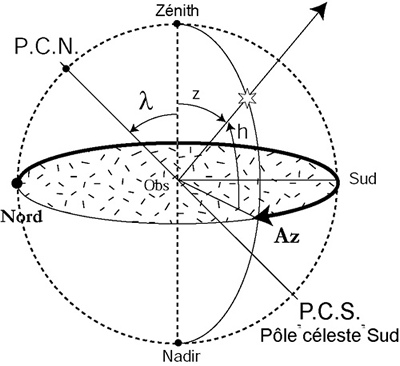 Repérage
Repérageh hauteur z distance zénithale (90 - h)
Az azimut: à partir du Nord vers lest de 0° à 360°
Les astronomes prennent pour convention Az à partir du sud vers louest (donc même sens) de 0° à 360°
l latitude du lieu
d déclinaison
AH angle horaire : de 0à 360°, sens rétrograde
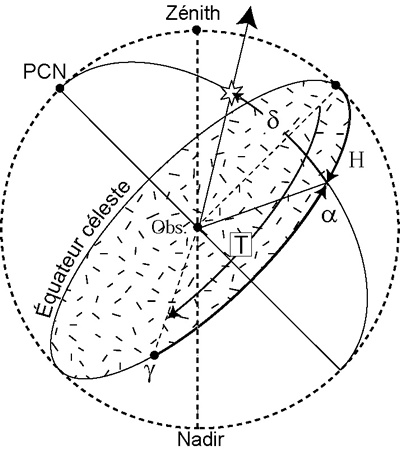 |
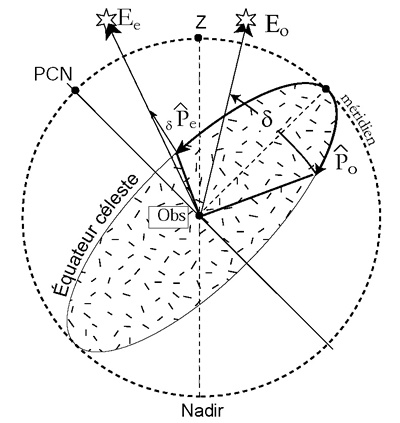
![]() :
angle au pôle : de 0 à 180° à partir du méridien P= AH si astre vers louest
P=360-AH si astre vers lest
:
angle au pôle : de 0 à 180° à partir du méridien P= AH si astre vers louest
P=360-AH si astre vers lest
d : déclinaison a : ascension droite variant de 0° à 360°
T Temps sidéral : angle horaire du point g (l'origine des ascensions droites)
![]() :
angle au pôle:
:
angle au pôle: ![]() =AH
si lastre est observé vers louest,
=AH
si lastre est observé vers louest, ![]() =
360° - AH si lastre observé vers lest
=
360° - AH si lastre observé vers lest
Formule de Charles Borda (1733-1799) donnant langle au pôle simplement
![]() avec S=(90-d+l+H)/2
avec S=(90-d+l+H)/2
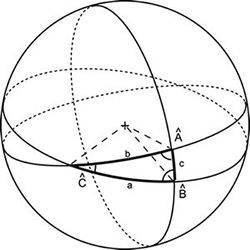 Faire le point
Faire le pointcosa = cosb * cosc + sinb*sinc*cosA
![]()
L la longitude en degré, L<0 à lest de Greenwich, L>0 à louest de Greenwich
Un jour à un instant T.U. , les éphémérides nautiques donnent, pour différents astres (soleil, lune ) :
· la déclinaison d de cet astre
· Son angle horaire, AHG pour un observateur situé sur le méridien de Greenwich
Pour un observateur situé à la longitude L, langle horaire est AHL= AHG L
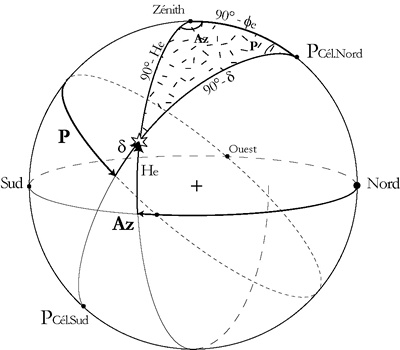
cos(90-He) =cos(90-fe)*cos(90-d)
+ sin(90-fe)*sin(90-d)*cos![]()
soit
sinHe= sinfe*sind
+ cosfe*cosd*cos![]()
![]() langle
au Pôle:
langle
au Pôle: ![]() varie
de 0 à 180° (Est ou Ouest)
varie
de 0 à 180° (Est ou Ouest)
d déclinaison de lastre
fe la latitude
F cos(90-d) =cos(90-fe)*cos(90-He) +
sin(90-fe)*sin(90-He)*cosZ
sind = sinfe*sinHe + cosfe*cosHe*cosZ
soit ![]()
Az est compté ici, comme le font les marins, avec une origine au Nord (Az=0°) De plus, dans la formule, la valeur de Az est comprise entre 0° et 180° ; pour en déduire la valeur réelle de lazimut comprise entre 0° et 360°, il faut savoir si lon observe vers lest ou vers louest
Les logarithmes inventés par John Napier (1550-1617) avec les tables publiées dès 1624 permirent de trouver plus facilement langle horaire que par la formule précédente (les multiplications deviennent des additions)
![]() avec S=(90-d+l+H)/2
avec S=(90-d+l+H)/2
H hauteur mesurée, d déclinaison
de lastre (lue dans les tables), l
latitude connue (déterminée à midi par exemple). On calcule donc
![]() ,
on en déduit langle horaire AHL de lastre à la longitude L, on
lit sur les tables quel est langle horaire AHG pour un observateur
placé sur le méridien de Greenwich et on en déduit la longitude par AHL=
AHG L
,
on en déduit langle horaire AHL de lastre à la longitude L, on
lit sur les tables quel est langle horaire AHG pour un observateur
placé sur le méridien de Greenwich et on en déduit la longitude par AHL=
AHG L
Avantage : observation sur le soleil ou la lune à toute heure du jour, sur les étoiles ou la lune la nuit
Contrainte : des calculs de trigonométrie sphérique
Lobservateur connaît approximativement sa position : Pe = position estimée
Méthode graphique et utilisant des tables (ou calculette): plus rapide elle remplacera la méthode de Borda au 19ème siècle
Au début du 19ième une nouvelle méthode avec logarithmes et construction graphique fut trouvée
Le cercle de hauteur, de rayon très grand est, à proximité du point estimé, assimilable à une droite
Soit He, la hauteur de lastre calculée à partir de la position estimée Pe (cest la hauteur de lastre que mesurerait un observateur réellement situé en Pe ; elle est donnée par la FormuleVIII-3-a)
Soit Az lazimut de lastre (observé au compas ou calculé à partir de Hv) ; deux cas sont possibles
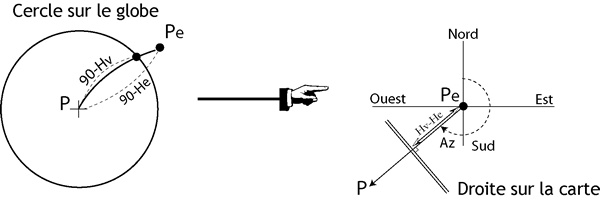
Figure 1 : Si Hv>He le point estimé est à lintérieur du cercle
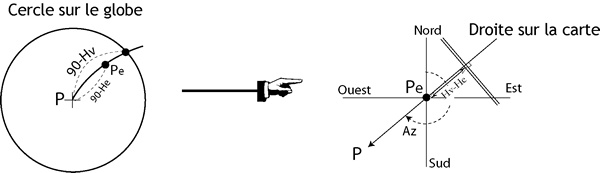
Figure 2 : Si Hv<He le point estimé est à lextérieur
du cercle
le 16 mai 2001 on mesure à 12h18 HLF une hauteur du soleil: 58°57' (corrigé de la réfraction et ½ diamètre)
donné par le logiciel pour Ternay (-4°50'Est, 45°35' Nord) qui donne aussi pour azimut 141°46'
Point estimé: Observatoire :Latitude: 50,80gr N (45°43') Longitude: 2,70gr Est de Paris (4°46' Est de G)
Heure de visée en T.U.: 12h18 HLF soit 10h18mn T.U.
Les éphémérides nautiques donnent d'heure en heure, chaque jour de l'année en cours, les coordonnées de la lune, du soleil des planètes et des étoiles. Pour le soleil elles donnent sa déclinaison et son angle horaire à Greenwich AHVO: angle horaire du soleil vrai à Greenwich (vo) (AH local se note AHVL)
|
16 mai 2001 |
AHVO |
Déclinaison du Soleil d€ |
||
|
heure T.U. |
degré ° |
minutes ' |
secondes" |
|
|
0h00 |
180°54' |
19 |
3 |
45,1 |
|
10h00 |
330°54' |
19 |
9 |
30,8 |
|
11h00 |
345°54' |
19 |
10 |
5,2 |
|
12h00 |
0°54' |
19 |
10 |
39,6 |
La table ne comprenant que des nombres entiers pour les déclinaisons, on arrondit au degré inférieur
Déclinaison arrondie du soleil 16 mai à 10h18 T.U.: d€=19°N: c'est la première clef
Latitude du point arbitraire (la plus proche du point estimé avec un nombre entier de degré)
Point estimé: 45°43' on prendra pour Latitude arbitraire 46°N c'est la deuxième clef
Le 16 mai à 10h00 T.U. AHVO=330°54'. L'angle horaire du soleil augmente d'environ 15° par heure soit pour 18mn une augmentation de 15*18/60=4,5°=4°30' donc à 10h18 T.U. AHVO=335°24'
(Les tables d'interpolation des éphémérides nautiques évitent la multiplication et la division ci-dessus)
AHVL = AHvo L (L<0 à l'Est de Greenwich, >0 à l'Ouest de G)
On choisit une longitude arbitraire la plus proche possible de la longitude estimée pour que l'angle horaire local AHVL soit un nombre entier. Ici on prend donc 4°36' pour que AHVL=340° C'est la troisième clef
(Volume 2: latitude 0° à 38°, déclinaison 0° à ±29°; volume 1: pour tracer les droites de hauteur d'étoiles)
Page 46°N "Same" parce que l=46° Nord et d=19° Nord et AHVL=340° (AHL anglais)
On lit l'azimut Az=142° (noté Z) et la hauteur (notée Hc) h=58°22' (+53)
Si la déclinaison valait 20° Az vaudrait 141° on garde Az=142° pour 19°10'
Si la déclinaison valait 20° Hc vaudrait 59°15' ce qui donne les (+53') d'écart.
La table d'interpolation HO249 (TABLE 5 Correction to tabulated Altitude for minutes of declination) nous dit alors que pour 10' (d€=19°10') la correction est 10*(53/60)=9 on prendra Hc=58°22' +9'=58°31'
On compare avec Hm=58°57' mesuré ce qui signifie que l'on est 26 milles plus près du pied du soleil que ce que l'on pris arbitrairement à porter sur l'azimut 142°
On peut opérer sur le soleil (99% des cas), la lune, une étoile à plusieurs heures dintervalle et trouver lintersection des deux droites de hauteur (en théorie aussi avec une planète)
On peut aussi opérer sur deux étoiles différentes à un même instant
Les définitions liées au temps sont celles du site du Bureau des Longitudes, fondé le 7 messidor An III (27 juin 1795). Les premiers membres, au nombre de dix, furent les mathématiciens Lagrange et Laplace, les astronomes Lalande, Delambre, Méchain et Cassini, le botaniste Bougainville, Borda, le géographe Buache, le constructeur de télescopes Caroché.
· Échappement : contrôle la façon dont séchappe la force motrice vers lhorloge
· Horloge (Horologium= lire lheure): jusquau début du Moyen-Age le mot désigne la clepsydre ou le cadran solaire
· Heure : du latin Hora au départ la douzième partie de la journée solaire ou de la nuit : elle ne devient la 1/24 partie du jour (incluant la nuit) que vers 1330. Division du jour en 1/60 chez Ptolémée
· Minute : du latin médiéval « pars minuta prima » première petite partie dans la division sexagésimale de lunité. Elle ne devient une division de lheure quau 13ième siècle avec lhorloge mécanique
· Seconde : abréviation de « partes minutae secundae » 2ième opération dans la division sexagésimale de lunité.
· degré : ° : peut-être à lorigine hiéroglyphe représentant le soleil. Le degré comme la 1/360 partie du cercle est utilisé par Babyloniens et les Égyptiens (année de 365 jours en 12 mois de 30 jours +5 jours épagomènes)
· Unités de distance en navigation
F 1 mille marin= 1/60 darc de degré équatorial=1852m
F 1lieue = 1/20 darc de degré équatorial = 3 milles
F 1 mille terrestre =1 650 m
· Pourquoi le système duodécimal (base 12)
F
Facilité de diviser le cercle en 6 (corde = rayon) puis en 12
et lannée de 365 jours vaut environ 12 lunaisons
Les cadrans dhorloges qui apparaissent au Moyen-âge sont gradués comme les
cadrans solaires (en 24 parties)
F La division en décans (période de 10 jours en Égypte) fait quil y a 18 décans en rotation pendant la nuit mais seulement 12 pendant lobscurité donc 12 heures nocturnes. Il y avait aussi dix heures de jour et une heure correspondant à laube et 1 heure correspondant au crépuscule : soit 12 heures de jour, 12 heures de nuit
· Pourquoi le système sexagésimal (malgré de nombreuses justifications l'origine du système de base 60 reste un peu mystérieuse)
F décompte avec une main des unités, une main des dizaines
F décompte des phalanges des 4 grands doigts dune main
F plus petit nombre ayant 12 diviseurs : 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30, 60, comme 12 est le plus petit nombre ayant 6 diviseurs : 1,2,3,4,6,12
· Sphère céleste. Sphère de centre et de rayon quelconques dont les points servent à représenter les directions de l'espace: à toute direction D on associe le point d'intersection de la sphère céleste et de la demi-droite parallèle à D dont l'origine est le centre de la sphère.
· Système de référence inertiel (ou galiléen). Système de référence spatial privilégié en mécanique newtonienne, associé à une échelle de temps uniforme. Deux systèmes de référence inertiels se déduisent l'un de l'autre par un mouvement de translation de vitesse constante. C'est dans ces systèmes de référence que sont valables les lois fondamentales de la mécanique générale.
· Système de référence spatio-temporel. Système de référence utilisé en mécanique relativiste et dans lequel il n'y a plus de véritable séparation entre coordonnées spatiales et coordonnée temporelle (voir Temps-coordonnée). Dans le cadre de la relativité générale, il n'y a plus de système de référence universel mais des systèmes locaux. À l'intérieur du système solaire on peut ainsi établir la hiérarchie des systèmes de référence suivante: système barycentrique centré au barycentre du système solaire, héliocentrique centré au Soleil, local Terre-Lune centré au barycentre du système Terre-Lune, géocentrique centré au centre des masses de la Terre et topocentrique dont l'origine est un point de la surface terrestre.
· Temps atomique international (TAI). Coordonnée de repérage temporel établie par le Bureau international de l'heure sur la base des indications d'horloges atomiques fonctionnant dans divers établissements et dont l'unité est la seconde SI.
· Temps-coordonnée. En mécanique relativiste, la première coordonnée de l'espace temps divisée par la vitesse de la lumière. Dans un système de référence spatio-temporel barycentrique, le temps-coordonnée peut être interprété comme le temps qui serait indiqué par une horloge au repos par rapport au barycentre du système solaire et infiniment éloignée des planètes.
· Temps coordonnée barycentrique (TCB). Échelle de temps-coordonnée liée au système de référence spatio-temporel barycentrique qui remplace le Temps dynamique barycentrique TDB dans le système recommandé par l'UAI en 1991. TCB diffère du Temps terrestre TT par des termes périodiques, des termes séculaires et des termes de Poisson.
· Temps coordonnée géocentrique (TCG). Échelle de temps-coordonnée liée au système de référence spatio-temporel géocentrique. TCG ne diffère du Temps terrestre TT que par un terme séculaire.
· Temps de lumière. Temps mis par la lumière émise ou réfléchie par un corps céleste pour atteindre l'observateur placé sur la Terre. Ce temps peut être considéré comme constant pour une étoile donnée mais non pour un objet du système solaire.
· Temps des éphémérides (TE ou ET). Échelle de temps utilisée de 1952 à 1976 pour les théories dynamiques et jusqu'en 1984 pour les éphémérides des corps du système solaire. Elle est définie à partir de la théorie du mouvement de la Terre autour du Soleil de Newcomb. Cette échelle de temps est maintenant remplacée par les échelles de Temps terrestre TT, de Temps Coordonnée Barycentrique TCB, de Temps Coordonnée Géocentrique TCG, de Temps Dynamique Barycentrique TDB.
· Temps dynamique barycentrique (TDB). Échelle de temps-coordonnée recommandée par l'UAI en 1976 pour les éphémérides et les théories dynamiques rapportées au barycentre du système solaire. TDB diffère du Temps terrestre TT par des termes périodiques et des termes de Poisson. En 1991, l'UAI a recommandé de remplacer TDB par le temps coordonnée barycentrique TCB.
· Temps propre. En mécanique relativiste, le temps lu sur une horloge dans un laboratoire. Il est différent du temps coordonnée.
· Temps sidéral en un lieu donné, à un instant donné. Angle horaire de l'équinoxe . On parle du temps sidéral vrai lorsqu'il s'agit de l'équinoxe vrai et du temps sidéral moyen lorsqu'il s'agit de l'équinoxe moyen de la date. En un lieu donné, à un instant donné, la somme de l'ascension droite vraie d'un astre et de son angle horaire est égale au temps sidéral vrai. Au moment du passage supérieur d'un astre au méridien, son ascension droite vraie est donc égale au temps sidéral vrai.
· Temps solaire moyen. Temps solaire vrai corrigé des inégalités de l'ascension droite du Soleil: c'est donc la partie linéaire, par rapport au temps, du temps solaire vrai.
· Temps solaire vrai en un lieu, à un instant donné. Angle horaire du centre du Soleil en ce lieu, à cet instant.
· Temps terrestre (TT). Échelle de temps utilisée pour les éphémérides géocentriques apparentes dont l'unité de temps est la seconde SI. Au 1 janvier 1977 0 h TAI, TT a pour valeur 1 janvier 1977, 0 h 0 min 32.184 s. C'est une échelle de temps idéale dont la réalisation pratique est liée au Temps atomique international TAI, par TT = TAI + 32.184 s.
· Temps universel (TU ou UT). Échelle de temps étroitement liée à la rotation diurne de la Terre qui a longtemps été à la base des temps légaux. TU est défini par une relation mathématique donnant l'expression du temps sidéral en fonction du Temps universel. On peut donc déterminer TU à partir d'observations d'étoiles (passage d'étoiles au méridien, par exemple). Le Temps universel ainsi obtenu est rapporté à un pôle fixe sur la Terre et est noté UT0. Le Temps universel rapporté au pôle céleste des éphémérides CEP s'obtient en s'affranchissant du mouvement du pôle et est noté UT1. Depuis 1984 l'échelle de temps légale n'est plus basée sur le Temps universel mais sur le Temps universel coordonné UTC.
· Temps universel coordonné (UTC). Échelle de temps diffusée par les signaux horaires et utilisée comme base des temps légaux. C'est, en fait le Temps atomique international TAI décalé d'un nombre entier de secondes. Ce nombre est modifié régulièrement de telle sorte que la différence entre UTC et le Temps universel UT1 n'excède pas 0.9 s en valeur absolue.
F Besançon : Musée du Temps, 1 place du Théâtre, 25 000 Besançon
F Briançon : Musée du temps (particulièrement de cadrans solaires)
F Le Locle : Musée dHorlogerie
F Cluses: Musée du Décolletage et de lHorlogerie, Espace Carpano et Pons, 74 300 Cluses 1h-12h 14h17h sauf Dim
F Villers le Lac: Musée de la Montre, 5 rue Berçot, 25 130 Villers le Lac Tél : 03 81 68 08 00
F La Chaux de Fonds, Suisse : Musée International dHorlogerie, 29 rue des Musées, Tél : 00 41 32 967 68 61
F Nuremberg : Germanisches NationalMuseum
F Leyde (Pays Bas) : Musée dHistoire des Sciences
F Londres : Science Museum
F Wuppertal: Historisches Uhrenmuseum
· Brest : Château de Brest, 29 200, Musée de la Marine Tel: 02 98 22 12 39 Fax: 02 98 43 30 54
F Du 1er octobre au 31 mars : 10h à 12h et de 14h à 18h, tous les jours sauf le mardi.
F Du 1er avril au 30 septembre : 10h à 18h30 tous les jours sauf le mardi matin.
· Paris : Musée de la Marine, Palais du Trocadéro
· Greenwich
· Amsterdam
· Les découvreurs, Daniel Boorstin, Robert Laffont
· Lheure quil est, David LANDES, Gallimard
· Longitude, Dava SOBEL, Seuil Points Sciences
· Histoire du point en mer, André GILLET, Belin Pour la Science
· Navigation astronomique, Patrick BRASSIER, Vuibert
· Étoiles et point astro, Voiles et Voiliers, Hors série n°10, 35F, 55 avenue Kléber 75 016
· Le point astronomique, Editions Chiron
· Tours du monde extraordinaires, Voiles et Voiliers H.S. n°3
· Japprends à faire le point, Voiles et Voiliers, H.S. n°8
· Japprends la météo, Voiles et Voiliers, H.S. n°11
· Astronomie et ordinateur, Dunod, un chapitre et trois programmes en Basic pour faire le point
[1]Les vers suivants sont attribués au poète Guyot de Provins (vers 1150) ou Hugues Bertius (vers 1250)
Un art font, qui mentir ne peut
Par vertu de la marinette,
Une pierre laide et noirette
Où le fer volontiers se joint