Un article de Jaubert et Holdsworth dans Nature Physics
Voilà près d'un siècle que Dirac a prédit l'existence d'un équivalent magnétique aux charges électriques qui nous entourent dans la nature, mais aucun de ces « monopoles » n'a encore été observé. Cependant, Castelnovo et al. (Nature, 451, 42, 2008) ont récemment mis en évidence la présence d'un analogue classique à ces étranges particules dans un matériau appelé la « glace de spin ».
Les propriétés étonnantes de ce composé viennent de son état fondamental fortement dégénéré qui joue le rôle de « vide », duquel peuvent émerger des paires de monopoles de charges topologiques opposées, sous forme d'excitations à très basse température (~ 1 Kelvin). Ces particules effectives ne modifient pas les équations fondamentales de Maxwell, mais interagissent par un potentiel coulombien d'origine magnétique comme les monopoles de Dirac.
Dans l'article qu'ils viennent de publier dans Nature, Ludovic Jaubert et Peter Holdsworth du laboratoire de Physique de l'ENS, montrent que des mesures de relaxation magnétique dans un matériau de glace de spin (Dysprosium Titanate, cf. Snyder et al. Phys. Rev. B, 69, 064414, 2004) s'explique en bonne approximation par la dynamique de ces monopoles se propageant dans un réseau effectif de « cordes de Dirac ».
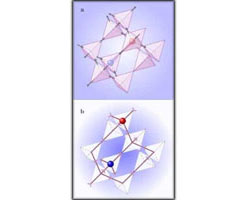
LÉGENDE DE L'ILLUSTRATION - Géométrie de la glace spin et émergence des monopoles :
a) Les ions magnétiques reposent sur les sites d'un réseau dit « pyrochlore » et doivent s'aligner le long du réseau diamant réciproque (pointillés). Les excitations locales « 3 in - 1 out » ou « 3 out - 1 in » correspondent à des monopoles magnétiques de charge positive (bleue) ou négative (rouge).
b) Le réseau diamant sert de squelette au réseau de « cordes de Dirac » avec la position des monopoles restreints aux vertex. L'orientation des cordes de Dirac correspond à la direction locale des lignes de flux magnétiques.