|
| |
Vous trouverez ici une liste
non exhaustive des thèmes fédérateurs proposés lors de la demande de
financement, les sujets abordés pouvant évoluer en fonction de l'intérêt porté à
de nouveaux sujets par les membres, et une présentation des actions envisagées.
Problématique générale
Les systèmes "hors-équilibre" sont actuellement l'objet d'un grand nombre
d'études des points de vue tant expérimentaux que théoriques, ce qui s'explique
en partie par le fait qu'ils concernent un grand nombre de domaines
d'application, de la physique de la matière condensée à la biologie, en passant
par l'hydrodynamique et la géophysique, par exemple. Malgré leur grande
diversité, ils ont tous en commun de présenter une comportement global complexe
dû aux interactions entre le composants élémentaires.
On peut à ce point distinguer deux types de système "hors-équilibre" :
-
Un système présentant un
dynamique lente bien que la dynamique à l'échelle microscopique soit
réversible. Le système possède un réel état d'équilibre qui n'est cependant
jamais atteint parce que certains degrés de liberté présentent une dynamique
trop lente pour que l'état d'équilibre soit atteint dans le temps
expérimental. Le système étudié se trouve donc dans un état
hors-équilibre qui évolue donc lentement dans le temps, ce qui est
communément dénommé par le terme vieillissement.
-
Un système présentant une
dynamique forcée. La dynamique à l'échelle microscopique est irréversible,
soit à cause du forçage, soit à cause d'une irréversibilité à l'échelle
microscopique (dans ce cas, le forçage est nécessaire au maintien du système
dans un état dynamique). On pensera ici, par exemple, à un matériau
conducteur soumis à un champ électrique ou, encore, à un gaz granulaire dans
lequel les interactions entre les grains sont dissipatives. Le système
atteint généralement un état stationnaire hors-équilibre.
Dans ces systèmes hors-équilibre les non-linéarités induisent
d'importantes fluctuations spatio-temporelles, des hétérogénéités spatiales, des
phénomènes de localisation dans l'espace. Ces hétérogénéités peuvent à leur tour
avoir pour conséquence un ralentissement de la dynamique (vieillissement). La
dissipation, si elle n'est pas intrinsèque, peut résulter d'un transport
non-linéaire de l'énergie des grandes vers les petites échelles. Plus
généralement, il peut en être de même pour d'autres grandeurs globalement
conservées, ce qui peut expliquer les spectres des fluctuations observés.
La compréhension de ces systèmes nécessite le développement de nouvelles
méthodes théoriques ainsi que l'apport de résultats expérimentaux. Les questions
ouvertes sont nombreuses. Par exemple: Comment les comportements de ces systèmes
dépendent du type de non-linéarité impliquée? Quel est l'impact de ces
non-linéarités sur les propriétés des grandeurs statistiques globales? Dans
quelles limites peut-on utiliser des relations de fluctuation-dissipation
généralisées?
Dans la suite, nous présentons de manière plus détaillée quelques thèmes
fédérateurs au centre de l'activité du GDR PHENIX. Cette liste ne se veut pas
exhaustive.
Propriétés statistiques des fluctuations hors de l'équilibre.
Différentes formulations des théorèmes de fluctuations ont apporté à la physique
statistique des résultats théoriques valables arbitrairement loin de
l'équilibre. Ces théorèmes décrivent quantitativement la symétrie de la
distribution du courant d'entropie qui se réduit parfois à la puissance injectée
dans le système. Ainsi, il a été montré expérimentalement que la propriété de
symétrie de Gallavotti-Cohen-Evans est vérifiée de manière exacte sur des
systèmes Langevin. Son application dans le cadre des systèmes dynamiques est en
revanche moins assurée, dans la mesure où il est très difficile de dire si les
résultats expérimentaux sont liés au théorème ou à la théorie de fluctuations
extrêmes. Par ailleurs le théorème de Gallavotti-Cohen considère la contraction
du volume dans l'espace des phases, une quantité non mesurable.
Pour les états stationnaires de non équilibre, il faut citer aussi les travaux
du groupe de Jona-Lasinio, sans oublier les travaux plus mathématiques issus de
modèles stochastiques. Ils ont montré que les fluctuations autour de la valeur
moyenne mettent en évidence des corrélations à longue portée, à cause de
l'existence d'une hydrodynamique adjointe non locale. Peut on obtenir ces
théorèmes par des projections de la dynamique, souvent plus claire ?
Par ailleurs, en 1997, Jarzynski a proposé dans le même esprit et en lien avec
les théorèmes précédents, une égalité statistique qui relie une grandeur
d'équilibre, la différence d'énergie libre entre deux états A et B, aux
résultats de mesure hors-équilibre. En notant W, le travail fourni pour passer
de l'état A à l'état B le long d'un chemin quelconque, l'égalité de
Jarzynski s'écrit
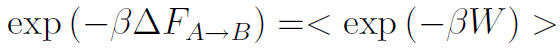où les crochets signalent la moyenne d'ensemble. La démonstration de cette
égalité suppose un système Hamiltonien, initialement thermostaté dans l'état A.
Expérimentalement, les systèmes étudiés jusqu'à présent étaient dissipatifs,
mais pouvaient être considérés sous une approximation Hamiltonienne. Néanmoins,
seuls des systèmes pouvant être formalisés par une équation de type Langevin ont
été étudiés expérimentalement. Les tests expérimentaux de l'égalité sont donc
plus réduits que ceux des théorèmes de fluctuations.
Un second problème de taille concernant l'utilisation de cette égalité provient
de la convergence très lente des statistiques qu'elle implique: il ne s'agit pas
de voir converger la moyenne du travail W, mais la moyenne de son exponentielle;
ainsi, une petite fluctuation négative (W < OF) sera surpondérée
exponentiellement. Si les fluctuations du travail ont une variance trop grande,
l'expérimentateur devra donc réaliser la même expérience des millions de fois
plus pour obtenir une moyenne correcte de l'exponentielle de W qu'il ne doit en
réaliser pour obtenir une moyenne correcte de W. Néanmoins l'inégalité de Crooks
permet de résoudre a priori ce problème. De nombreuses expériences restent
encore à faire dans ce contexte.
Ces questions sont tout à fait cruciales dans le contexte du vieillissement, des
milieux granulaires, de la dynamique près d'un point critique ou dans le cadre
hydrodynamique.
L'étude des grandes déviations temporelles est en plein essor. Elle est motivée
par son approche globale, ce qui permet de faire un lien avec de nouvelles
approches expérimentales. L'autre motivation est théorique, par la construction
d'une mécanique statistique où l'enjeu est la connaissance de quantités
extensives dans le temps, par analogie avec une mécanique statistique à
l'équilibre qui s'intéresse aux quantités extensives dans le nombre de degrés de
liberté. Le nombre de travaux théoriques convaincants, et de dérivations exactes
augmente dans ce domaine, et ces recherches méritent d'être poursuivies.
L'interaction entre systèmes dynamiques et physique statistique a aussi permis
de nouveaux développements concernant les grandes déviations temporelles;
notamment par l'extension du formalisme thermodynamique de Ruelle (ou
thermodynamique des histoires) aux systèmes Markoviens. Un thème en émergence
est celui des systèmes vitreux, où les fonctions de grandes déviations
temporelles et la validité éventuelle d'un théorème de fluctuation sont encore
mal connues.
Physique
statistique et dissipation.
En présence de dissipation, la dynamique microscopique est irréversible et il
est nécessaire de forcer le système pour établir un état dynamique stationnaire
hors équilibre. Il existe alors en général un transfert d'énergie, voire
d'autres quantités conservées, au travers des échelles du système considéré. La
distribution des fluctuations de ces quantités entre les grandes et les petites
échelles d'une part, leur localisation spatiale - en général hétérogène -
d'autre part, résultent à la fois des interactions non-linéaires et de
l'équilibre qui s'instaure à chaque échelle entre le flux transféré entre les
échelles et le flux dissipé vers l'extérieur. Dans la mesure ou ce flux est tout
sauf un équilibre thermique avec l'environnement, on comprend immédiatement que
l'étude de ces systèmes est intimement liée à celle du couplage avec
l'environnement. A titre d'exemple, si on vibre une plaque dans l'air la
dissipation aura lieu selon de nombreux modes hydrodynamiques à grande échelle,
suivis de modes sonores à plus petite échelle pour finalement exciter des modes
de rayonnement en échauffant la plaque à toute petite échelle. On voit bien que
la même plaque excitée dans le vide n'aura pas du tout le même spectre
d'énergie, puisque seul les modes radiatifs à petite échelle pourront être
excités. On rencontre ce type de situation dans de très nombreux systèmes, de la
turbulence d'onde aux liquides granulaires.
Pour exemple, parmi les avancées notables de ces dernières années dans l'étude
des milieux granulaires nous retiendrons tout particulièrement celles de type
"premiers principes", et en particulier l'obtention d'équations hydrodynamiques
fermées pour les gaz granulaires. Ces travaux, s'appuyant sur la théorie
cinétique mais limités pour des raisons techniques aux gaz dilués, sont appelés
à être étendus aux systèmes plus denses avec comme but ultime la rhéologie des
écoulements granulaires génériques, même si la controverse concernant le domaine
d'applicabilité des techniques employées est toujours d'actualité. Pour autant,
ces travaux ont permis d'expliquer un certain nombres d'observations
expérimentales faites sur les lits fluidisés. Certaines de ces observations,
parfois contre-intuitives, avaient été initialement considérées comme
"aberrantes" (l'inversion du profil de température granulaire dans un système
vibré confiné par la gravité est un bel exemple). On peut espérer à moyen terme
comprendre le régime non newtonien des gaz granulaires, qui constitue la règle
plus que l'exception même pour les systèmes les plus simples ou les plus
"modèle", comme les sphères dures inélastiques. Il s'agit là d'une différence
notable avec les fluides ordinaires, qui n'a pourtant été formulée explicitement
que très récemment. Une approche de type milieux continus s'en trouve
singulièrement compliquée, mais c'est peut être là qu'une partie de l'effort va
porter dans les prochaines années, pour unifier la description des régimes
dilués et denses qui avaient jusqu'à présent été complètement déconnectés. Une
collection de grains peut aussi sous certaines conditions d'excitation mécanique
atteindre un régime stationnaire, pour lequel l'énergie apportée est exactement
compensée par les différents modes de dissipation. Dans ce régime, des grandeurs
moyennes telles que volume, contraintes, déformations peuvent être définies à
l'échelle de l'échantillon de grains et on peut espérer obtenir des relations
thermodynamiques entre elles, dans l'esprit des travaux d'Edwards, mais aussi
tester expérimentalement les hypothèses sous-jacentes.
Enfin, l'étude des systèmes dissipatifs peut s'aborder au travers de systèmes
modèles pour lesquels on peut calculer explicitement la distribution
stationnaire et étudier ses propriétés dans les régimes de faible ou forte
dissipation. En effet rien n'assure par exemple que la limite de faible
dissipation et donc de faible forçage, soit une situation équivalente à celle
d'équilibre. Cette propriété peut en particulier dépendre du système considéré
et de son environnement. Il est d'autant plus crucial de connaître les cas où
cela serait le cas, dans la mesure où il existe alors toute une méthodologie
inspirée de la physique statistique des systèmes à l'équilibre pour évaluer les
états stationnaires et les propriétés de relaxation à leur voisinage.
Dynamique non-linéaire de systèmes avec forces à longue portée.
Une interaction est à longue portée si son énergie diverge plus vite que le
volume: elle est, par conséquent, non additive. Parmi les nombreux exemples, on
peut citer la gravité, les interactions coulombiennes non-écrantées, les
interactions dipolaires, les interactions ondes-particules. Ces systèmes, a
priori très différents, présentent des similarités. Ils peuvent être le siège de
comportements thermodynamiques inhabituels, tels que chaleur spécifique
négative, inéquivalence d'ensembles statistiques, mais aussi de phénomènes
dynamiques étonnants.
La compréhension de la dynamique et de la thermodynamique de ces systèmes, ainsi
que des analogies et différences entre les systèmes physiques concernés, a connu
récemment un nouvel essor, impliquant des chercheurs venant d'horizons variés.
De nouvelles applications de la mécanique statistique d'équilibre ont été
proposées. Les propriétés d'équilibre statistique ont ainsi été étudiées pour
des systèmes autogravitants, dans des modèles effectifs de lasers, dans le cadre
d'écoulements géophysiques ou en relation avec la magnéto-hydrodynamique, dans
le cadre de modèles de spins ou de rotateurs. Les aspects de dynamique non
linéaire ont été aussi abordés par l'intermédiaire d'approches cinétiques, dans
le cas des points vortex, des équations d'Euler ou de modèle simples de
particules.
Si certaines questions concernant l'équilibre statistique restent ouvertes, en
ce qui concerne par exemple la compétition entre plusieurs types d'interactions,
à courte et longue portée, les aspects dynamiques offrent beaucoup de questions
intéressantes: la dynamique lente de la relaxation vers l'équilibre, une
paramétrisation des petites échelles basée sur la mécanique statistique dans le
cas des systèmes fluides, la description statistique de l'évolution sur des
échelles de temps long de tels systèmes (échelles de temps climatiques pour des
modèles simplifiés d'océans ou d'atmosphères), la description statistique des
fluctuations au voisinage de transitions de phases et de multistabilités.
Un autre enjeu des années à venir sera le renforcement des liens entre les
théories et les différents domaines concernés de la physique. On peut espérer
des applications pour les océans et atmosphères terrestres, pour des modèles de
laser type CARL, pour des problèmes de magnétohydrodynamique et de mécanique des
fluides, pour des problèmes de matière condensée, pour des molasses optiques
d'atomes froids à forte densité, des tubes à ondes progressives, des systèmes de
type laser à électrons libres...
Ce retour vers les domaines d'application devrait également stimuler les
développements théoriques dans de nouvelles directions, souvent en lien avec la
physique hors équilibre du type "dynamique forcée'': systèmes non conservatifs,
bruits corrélés, transitions de phase induites par le bruit... Il y a là un gros
potentiel de développement pour cette thématique.
Dynamique non linéaire sur réseaux statiques, dynamiques, réguliers ou
complexes.
Une représentation sur réseau est particulièrement adaptée à de nombreux
systèmes touchant à des domaines d'application variés (réseaux de neurones ou
réseaux d'interactions entre gènes et protéines à l'intérieur de la cellule,
macromolécules biologiques, dynamique forestière, internet, réseaux électriques,
les transports, etc.) Un système est alors décrit comme un ensemble de sites ou
sommets reliés par des liens. Le choix de systèmes à espace-temps discret pour
modéliser des systèmes étendus permet, en particulier, de représenter
simplement, à la fois des effets de retard et des interactions intégrales (par
opposition à locales) dans l'espace.
La recherche dans le domaine des réseaux comporte de nombreux aspects dont nous
retiendrons ici l'étude des phénomènes dynamiques qui y prennent place. De
nombreuses questions restent ouvertes. Quelles sont, par exemple, les
conséquences des propriétés et, éventuellement, de la dynamique du réseau
lui-même, sur la dynamique du système?
Dans le cas des systèmes dissipatifs, on sait maintenant caractériser
relativement bien les régimes extrêmes (description géométrique et statistique,
e.g. propriétés topologiques du chaos spatio-temporel, phases de faible
couplage, synchronisation globale) ou de certaines parties de l'espace de phase
(formation et dynamique de structures, synchronisation partielle). On sait
également aller plus loin, c'est-à-dire décrire des changements de régimes pour
des modèles particuliers et dans certaines expériences (instabilités de Faraday,
optique non-linéaire). Cependant le problème de la description de routes
génériques reliant les régimes de chaos spatio-temporel à ceux de
synchronisation dans des systèmes dissipatifs reste ouvert. Quels sont les
analogues, pour les systèmes étendus, des fameuses routes vers le chaos ?
Dans le cas de systèmes présentant une architecture complexe (un désordre
structurel par exemple) ou des interactions non-linéaires entre sites, on peut
s'interroger sur l'apparition d'effets de localisation de l'énergie, sur la
statistique des fluctuations, sur l'existence d'états transitoires de longue
durée,... De tels modèles ont de nombreux domaines d'application, en
particulier, en biologie (macromolécules, réseaux de neurones, processus de
régulation,...). Enfin, signalons aussi l'importance des fluctuations pour des
systèmes dans lesquels les acteurs sont peu nombreux (fluctuations importantes
dans la dynamique des processus de régulation dues au faible nombre de certaines
espèces dans la cellule), cas dans lesquels le champ moyen n'est pas
nécessairement applicable.
Les actions
Réunions plénières.
Il est nécessaire de donner, une fois par an à l'ensemble des membres du GDR
PHENIX, l'occasion de connaître les derniers résultats obtenus dans les équipes
participantes. De plus, au cours de ces réunions plénières, une partie du temps
(typiquement une demi-journée) pourra être consacrée à l'enseignement de
concepts généraux propres à chaque communauté afin d'asseoir une base culturelle
commune et de former les jeunes chercheurs (en particulier les doctorants). On
choisira pour ces réunions, d'une durée typique de trois jours, un lieu propice
aux interactions informelles qui, on le sait, favorisent la naissance des
nouvelles
idées et l'émergence des collaborations.
Ateliers thématiques.
Nous organiserons, par ailleurs, un minimum de deux ateliers thématiques par an.
Ces ateliers rassembleront un nombre réduit de participants (typiquement 20) qui
seront appelés à discuter en profondeur d'un sujet précis au cours d'une journée
thématique. La journée consistera en une discussion libre autour d'une trame
préétablie par son organisateur, chaque participant intervenant librement dès
qu'il dispose d'éléments ou de résultats à apporter au débat. Il ne s'agira donc
pas ici de proposer une série d'exposés programmés. Cependant, la journée pourra
être l'occasion d'inviter un spécialiste à donner un exposé en ouverture à la
discussion. Nous inciterons les membres du GDR PHENIX à suggérer les sujets
traités au cours de ces journées qui permettent, par la confrontation de
résultats et par la discussion, d'apporter un regard nouveau sur des choses
éventuellement connues par ailleurs et d'identifier clairement les points bien
compris et les questions ouvertes.
Soutien à la mise en place de projets.
Le GDR PHENIX a pour vocation non seulement d'encourager mais aussi de
pérenniser les interactions entre les participants. Afin d'encourager les
collaborations effectives, il pourra éventuellement apporter son soutien à des
missions entre les équipes impliquées dans des demandes de financement (projets
ANR, projets européens, etc.)
Diffusion de l'information et annonces
Le GDR PHENIX dispose déjà d'un système de diffusion efficace basé sur une large
liste de diffusion et un site internet. Ces outils permettent, en plus de
diffuser les informations propres à l'organisation des réunions, de collecter
des annonces pouvant concerner les participants (thèses, post-doctorat,
colloques, etc.) Nous nous efforcerons seulement, sur la base de ce qui existe
déjà, de renforcer le caractère interactif du site internet en permettant, par
exemple, le dépôt d'information par les membres (manuscrits, articles, etc.)
|
