Astronomie dans l’Antiquité
1) Les instruments d’observation
1) Les théoriciens et observateurs grecs
1) Thalès de Millet (624 à 548)
2) Pythagore de Samos (569 à 500)
5) Œnopide de Chios (vers 450)
7) Anaxagore de Clazomène (500-428)
8) Platon d’ Athènes (427-347)
9) Aristote de Stagire (384 – 322)
10) Timocharis et Aristyle (vers
295-280 avant J.C.)
11) Aristarque de Samos (310-240)
14) Callippe de Cyzique, né vers
370
15) Apollonius de Perge (265-190)
16) Pythéas de Marseille (voyages
vers 330)
17) Erathostène de Cyrène(284 –
192)
18) Hipparque de Nicée (194 à 120)
19) Ménélaüs (vers 80 après J.C.)
20) Ptolémée (85 à 165 après J.C.)
d’ Alexandrie
21) Euclide de Cnide (315-255)
22) Archimède de Syracuse (287-212)
2) Hérodote d’ Halicarnasse
(484-420)
5) Théon d’Alexandrie (380 avant
J.C.)
9) Théon de Smyrne (2ème
siècle après J.C.)
13) Proclus (entre 400 et 485)
1) al Battâni Albatagnus (877-929)
III Timocharis,
Hipparque et la précession des équinoxes
4) Le point g à différentes époques
3) Époque de correspondance entre
les "signes..." et les constellations du zodiaque
I Introduction
Astronomie arithmétique des babyloniens, géométrique des grecs
Le plus ancien document d’astronomie de Babylone date de la période sumérienne de 2000 à 1600 dite paléo-babylonienne : de cette période sont parvenus des énumérations d’étoiles, de constellations, des prédictions associées à des éclipses de lune et des observations de Vénus
« Au 15e jour du mois, Vénus disparut. Durant trois jours elle resta absente du ciel. Puis le 18e jour du 11e mois elle reparut à l’est. Des sources jailliront, Adad enverra sa pluie ; Ea apportera ses crues… »
L’astrologie chaldéenne annonce surtout des évènements d’intérêt collectif (épidémie, inondations, guerres) alors que la prédiction dans une vie humaine apparaît en même temps en Perse et en Grèce vers 400. Elle connut une grande vogue sous Auguste
Astrologia est le terme classique pour désigner l’astronomie (Varron, Cicéron, Vitruve). Les auteurs chrétiens distingueront nettement astrologia et astronomia
Division babylonienne de la journée et de la nuit en douze parties, du zodiaque en douze parties à partir de 500. Auparavant division de l’écliptique en 36
Ptolémée regrettait de ne pouvoir disposer de documents mésopotamiens sur les positions des planètes, mais il possédait des tables d’éclipses remontant au règne de Nabossar (-700)
1) Les instruments d’observation
Gnomon
Clepsydre
Le polos : gnomon dont la pointe est au centre d’une ½ sphère (deviendra le scaphe)
La dioptre d’Archimède : viseur et cylindre mobile
La dioptre d’Hipparque : viseur à 1 fente , curseur à 2 fentes permettant de mesurer le diamètre apparent d’un astre (soleil ou lune) Ptolémée la trouve meilleure que la clepsydre
La latitude est désignée par le rapport du jour le plus long au jour le plus court 7/5 pour Alexandrie où le jour du solstice d’été dure 14 h et le solstice d’hiver 10h. Pour calculer le nombre d’heure de jours, il suffit d’évaluer le temps que met à se lever les 6 signes du zodiaque qui suiven,t le point o de l’écliptique où se trouve le soleil.
Pour évaluer le temps de lever des 12 signes du Zodiaque les astronomes grecs, à partir de l’Almageste, utilisent des calculs trigo complexes mais exact conduisant à un courbe à double bosse. A Babylone les temps de levers sont admis croissants du Bélier à la Vierge et décroissants de la Balance aux Poissons ce qui donne une courbe à une bosse
Les Babyloniens utilisaient déjà le gnomon certainement pour repérer les solstices.
héliotrope capable de montrer « les conversions du soleil » Homère
importance des solstices pour les travaux agricoles (Hésiode, Les Travaux vers 564-663)
ombre minimale diurne donne le midi
ombre méridienne minimale donne solstice d’été
ombre méridienne maximale donne solstice d’hiver
gnomon « qui sert à connaître »
un obélisque égyptien de 22m datant du pharaon Psammétique II fut placé d’abord à la périphérie de Rome puis ramené au champ de Mars par Auguste en 10 av JC (Pline l’Ancien, XXXVI chap 10)
Tour des vents d’Andronykos à Athènes du 1er siècle av JC : 8 faces surmontées de cadran et d’une frise d’un vent. Au sommet sculpture en bronze contenant une clepsydre
2) Le zodiaque
Problèmes : ajuster le calendrier lunaire au soleil
La pratique astrologique a conduit à jalonner la route du soleil de points de repères : d’abord des étoiles brillantes puis les constellations nommées depuis longtemps. La division en 12 signes de 30) est attestée vers –500 (peut-être même vers –1500). Sextus Empiricus présente deux « Chaldéens » dont l’un observe le ciel et l’autre se prépare à signaler la venue au monde du personnage dont on va faire l’horoscope
L’observation pure, sans aucun but prophétique est aussi appréciée « Mars est entrée dans la constellation d’Allul. Cela ne comporte aucun présage »
3) Les carnets de Babylone
observations ininterrompues de 650 à 150 av JC (mouvements de la lune et des planètes, temps, prix des produits, niveaux de l’Euphrate)
En particulier « disparition » des planètes, « changements de direction », distances à une trentaine d’étoiles de références mesurées en coudée (environ 2,5°)
Epoque séleucide de 300 à 150 : tablette donnant précisément la vitesse journalière du soleil dans chaque signe
Des papyrus égyptiens montrent que tout le système arithmétique babylonien à été transmis en Egypte hellénistique et que Hipparque en a certainement eu connaissance
II Les astronomes
1) Les théoriciens et
observateurs grecs
1) Thalès
de Millet (624 à 548)
d’origine phénicienne il fonde l’Ecole de Millet vers 587 (sur la côte ionienne)
Explique les éclipses, constate durée solstices été à hiver > solstice hiver à été
Théorèmes fondamentaux sur les angles
2 droites qui se coupent forment des angles opposés par le sommet égaux entre eux (utilisé par Anaximandre son disciple qui prend le milieu de l’arc inter-solsticial pour obtenir la longueur de l’ombre équinoxiale)
Proposition I, 9 des Eléments d’Euclide : partager un angle en deux égaux
Proposition les angles à la base d’un triangle isocèle sont égaux
Proposition les angles inscrits dans un demi-cercle sont droits (le gnomon et sont ombre peuvent jouer le rôle de cordes interceptant des arcs dont la somme forme une demi circonférence
Hérodote le crédite d’avoir prévu l’éclipse de soleil du 28 mai 585
Aëtius le crédite d’avoir le premier expliqué les phases de la lune « La lune est illuminée par le soleil »
L’univers est semblable à une bulle d’air dans un liquide infinie : La Terre est un cylindre plat flottant sur les eaux d’en bas (explique séismes, vents…), les astres flottent sur les eaux d’en haut
2) Pythagore
de Samos (569 à 500)
Elève de Thalès, d’Anaximandre, Egypte, captif à Babylone, retourne à Samos puis se fixe à Crotone vers –529 (Italie du Sud) ou il fonde son école où l’on étudiait philosophie, mathématiques, sciences naturelles et l’on pratiquait des rites tenus secrets
Livre I proposition 47 : théorème de Pythagore
Pythagore et ses disciple auraient découvert l’identité Vesper-Lucifer, l’obliquité de l’écliptique, l’ordre des planètes
Pour eux le monde est organisé autour d’un feu central autour duquel gravite 10 sphères de cristal séparés par des intervalles harmonieux : Antiterre, Terre, 7 planètes, étoiles fixes. Les astres renvoient la lumière du feu central
3) Anaximandre
(610 à 543)
Le premier à avoir enseigné que la Terre était le centre de l’univers (modèle de sphère probable)
La pointe du gnomon est l’image de la Terre flottant dans l’univers
Anaximandre aurait été le premier à percevoir les équinoxes
Doiogène Laerce lui attribue la connaissance de la variation de la longueur de l’ombre du gnomon en fonction de la latitude (II, 1) alors que Pline l’attribue à son élève Anaximène (II, 187)
Détermine l’arc entre les solstices
Met en évidence le rayon méridien équinoxial, la longueur de l’ombre méridienne et l’obliquité de l’écliptique
Représentation du monde issue du gnomon utile pour l’astronomie et la géographie
4) Parménide
d’Elée
5) Œnopide
de Chios (vers 450)
fixe la valeur de e à 24° soit le coté du pentadécagone (15 cotés)
Proclus lui attribue les propositions
Proposition 12 du Livre I : Tracer une perpendiculaire à une droite à partir d’un point hors de cette droite
Proposition 23 du Livre I : Sur une droite, et en un point de cette droite construire un angle donné
6) Anaximène
Vers 500 avant J.C., disciple d’Anaximandre
7) Anaxagore
de Clazomène (500-428)
Né près de Smyrne, le premier à expliquer les phases de la lune et les éclipses
Maître d’Euripide et de Périclès ;
Terre plate ou concave ?
8) Platon
d’ Athènes (427-347)
Disciple de Socrate, voyage en Orient, en Italie et en Egypte. De retour à Athènes vers 377 il fonde son école dans les jardins d’Académos où il enseigne pendant 40 ans .
Il n’apporte rien aux mathématiques, mais dans ses 43 écrits avec 121 passages se référent aux mathématiques La République, Phédon, Timée (polyèdres réguliers), Théétète , Epinomis
« Que nul n’entre ici s’il n’est géomètre »
Socrate dans Phédon 109
« Voilà donc ce quoi dont je me suis laissé convaincre. C’est tout d’abord que si la Terre est au centre du monde et qu’elle soit ronde, elle n’a nul besoin, pour éviter de tomber, ni de l’air, ni d’aucune pression du même genre. Mais ce qui suffit à la retenir, c’est la similitude de toutes les directions du monde entre elles et l’état d’équilibre de la Terre elle même ; car pour une chose qui est placé en équilibre au centre d’un contenant homogène, il n’y aura lieu, ni peu ni prou, de tomber d’aucun côté ; or une telle position étant celle de la Terre, étant incapable de tomber elle restera immobile. (cf Aristote De caelo I 13, 295 b qui se
Le second point maintenant poursuivit Socrate : c’est qu’il s’agit de quelque chose de tout à fait grand et dont nous qui habitons du Phase (extrémité Est de la Mer Noire) jusqu’aux colonnes d’Hercule n’occupons qu’une petite parcelle, logés à l’entour de la mer, fourmis ou grenouilles comme à l’entour d’une eau stagnante.
Voici ce que l’on rapporte: C’est d’abord que l’image de cette Terre, est à peu près celle-ci : un ballon bariolé pareil aux balles de peau à douze pièces et dont les quartiers se distinguent par des couleurs…
(dodécaèdre fait de douze pentagones Timée 55c et 97e)
9) Aristote
de Stagire (384 – 322)
Né à Stagire près du Mont Athos. Il fut élève de Platon et fonda le Lyceum.
Il donne des arguments tirés d’observation à la rotondité de la Terre annoncé par Pythagore
Alexandre de Macédoine son élève
Les Physiques (englobe astronomie et météorologie)
Traité du ciel
10) Timocharis
et Aristyle (vers 295-280 avant J.C.)
Cités par Ptolémée
Hipparque se serait servi de leurs observations d’éclipses pour découvrir la précession des équinoxes
11) Aristarque
de Samos (310-240)
études à Alexandrie dirige le Lycée d’Aristote à Athènes
Gnomon muni d’une scafe, (hémisphère concave)
Archimède nous apprend que Aristarque donnait pour le diamètre du soleil 1/720 zodiaque, et qu’il utilisait les fractions de zodion : « la lune sous tend 1/15 d’un zodion »
« Lorsque la lune nous apparaît dans sa moitié sa distance au soleil est de 1 quadrant moins 1/30 (87°) »
jusqu’à Euclide les angles sont mesurés en fractions de l’angle droit, 180° = deux angles droits, 60° = 2/3 droit, 30° = 1/3 droit, 72° = droit moins 1/5
La division du jour en 360° se trouve chez Hypsiclès vers –180
Chez Ptolémée, le cercle est divisé en 360° de 60’ de 60’’
12) Eudoxe
de Cnide (406-355)
élève d’Archytas de Tarente et de Platon
attribue la valeur 5/3 au rapport des arcs diurne et nocturne à Athènes
Il perfectionne le dioptre et l’arachné (il aurait inventé l’astrolabe sphérique)
Ecrit des parapegmes vers 370 intégralement connu
Son système de sphères homocentriques pour expliquer les mouvements des planètes, améliorée par Callippe et repris par Aristote domine la pensée scientifique jusqu’à Copernic
13) Méton
établit vers 432 son cycle de 19 ans (qui ne remplaça jamais l’octaétéride en usage)
14) Callippe
de Cyzique, né vers 370
élève de Polemarchos. Il améliore le système d’Eudoxe pour tenir compte de l’inégalité des saisons
Il étudie le calendrier et substitue une période de 76 ans au cycle de Méton. Il écrit un livre de parapegmes
15) Apollonius
de Perge (265-190)
Il vécut à Alexandrie, Éphèse, Pergame
Théorie des coniques
16) Pythéas
de Marseille (voyages vers 330)
Marseille fondée vers 600 par les Grecs
Il se sert du rapport gnomonique pour donner la latitude de Marseille : la plus ancienne attestation de mesure gnomonique pour donner la latitude : rapport 120/(42-1/5) = hauteur/ombre équinoxiale
Pythéas aurait composé en grec deux ouvrages dans lesquels il raconte ses voyages.
Dans sa Description de l’Océan, il relatait son voyage par mer depuis Gades (identifié comme étant Cadix), jusqu’à Thulé (Iles Shetland ou Islande). Après avoir contourné les Iles Britanniques par l’Ouest, il aurait remonté à nouveau la Manche jusqu’à la baie de Gdansk en mer Baltique. Etienne de Byzance, écrivain du Ve siècle, possédait encore ces écrits aujourd’hui disparus : il ne nous reste quelques citations souvent critiques d’auteurs prévenus contre Pythéas et qui lui prêtent leurs propres erreurs.
Strabon (Liv. II, p. 117) écrivait vers l'an 44 avant J. C. « il n’avait parcouru les pays dont il parle, vers le couchant, que depuis l’Arménie jusqu’à cette partie de la Toscane qui est en face de la Sardaigne; il s’était imaginé que le froid rendait la terre inhabitable au-dessus du 54e degré de latitude, et parce que les navigateurs de son temps ne dépassaient point l'Irlande, l’Hibernie, il se croyait en droit de traiter de mensonges tout ce Pythéas avait dit sur Thulé, l’Islande, et les mers du Nord.
Conversion de longueurs en angle
17) Erathostène
de Cyrène(284 – 192)
aurait étudié à Athènes puis invité par Ptoléme III a été directeur de la bibliothèque d’Alexandrie (vers 287-195) Livre Géographie en trois livres
Aristote cite des mathématiciens qui ont calculé la longueur d’un arc de grand cercle (De caelo,II 14 vers 297)
on cherchait à mesurer la différence entre deux horizons de lieux à distance connue
Canope invisible en Grèce, culmine à hauteur nulle à Rhodes, 1/48 cercle à Alexandrie située sur le même méridien ; donc la longueur
18) Hipparque
de Nicée (194 à 120)
Née à Nicée sur la côte de l’actuelle Turquie, il s’installe à Rhodes à 30 ans
Il perfectionne les instruments d’observation : dioptre, astrolabe ; il aurait systématisé la subdivision du cercle en 360°, et crée le 1er globe céleste
Théon d’Alexandrie lui attribue un traité en 12 livres sur le calcul des cordes
Il établit le premier catalogue d’étoiles (en coordonnées écliptiques)
Découvre la précession des équinoxes
Il étudie le calendrier: période de 304 ans plus précise que celle de Callippe, écrit un livre de parapegmes
Il développe un système planétaire à excentrique et épicycles qui sera repris par Ptolémée
Tous ces ouvrages sont perdus sauf une œuvre de jeunesse
19) Ménélaüs
(vers 80 après J.C.)
Connu pour son célèbre théorème des transversales dans un triangle plan ou sphérique
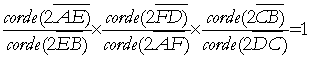 ou
ou 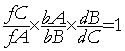
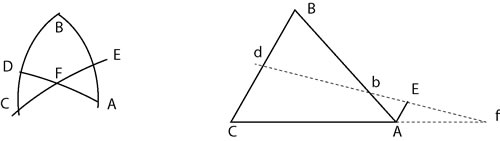
20) Ptolémée
(85 à 165 après J.C.) d’ Alexandrie
« Synthèse mathématique » de 13 livres appelée Almageste par les Arabes
Tables de cordes
Comment la durée du jour le plus long permet de déterminer la hauteur du pôle et réciproquement
21) Euclide
de Cnide (315-255)
sur le continent au Nord de l’Ile de Rhodes. Probablement élève de l’Académie d’ Athènes
Il aurait été invité par le Roi Ptolémée I Sôter, héritier de la partie égyptienne de l’Empire d’Alexandre, fondateur des institutions savantes (vers 300) d’Alexandrie (bibliothèque, université, observatoire).
Auteur d’une dizaine de traités dont « Les Eléments » divisé en 13 livres (géométrie plane, théorie des nombres, géométrie dans l’espace). Des dizaines de manuscrits en grec
Titre grec de stoicheia, les lettres comme éléments de la syllabe. Verbe steichô : avancer en rang (distique, stœchiométrie... )
Jusqu’en 1900, ouvrage le plus édité après la Bible, première édition de 1482
Proposition IV 16 : inscription du pentédécagone dans un cercle (comment prendre au compas 1/15 du cercle)
Alexandrie fondée par Alexandre en 322 fut dotée d’une
22) Archimède
de Syracuse (287-212)
il aurait été élève des meilleurs élèves d’Euclide à Alexandrie
2) Les commentateurs
1) Homère
(vers 750)
Originaire de Smyrne d’après Hérodote
2) Hérodote
d’ Halicarnasse (484-420)
Sa famille ayant été exilé par le tyran Lygdamis il voyage en Egypte, Perse, Syrie, rives de la Mer Noire
Fonde en 443 avec des Athéniens Thourioui sur les ruines de Sybaris en Italie (au pied de la botte)
Histoire Livre II, 109
Hérodote raconte comment les percepteurs égyptiens mesurent le terrain perdu par les paysans en raison des crues du Nil et diminuent la redevance au pro-rata. « C’est ce qui donna lieu, à mon avis à l’invention de la géométrie que des Grecs rapportèrent dans leur pays. Car, pour l’usage du polos, du gnomon et pour la division du jour en douze parties c’est des babyloniens que les Grecs les apprirent »
Indications babyloniennes inexactes sur les équinoxes
Livre III, 115 «des extrémités du monde qui se trouvent vers le couchant, je ne puis parler avec certitude ; car je n’admets pas, quant à moi, que des barbares appellent Eridan un fleuve se jetant dans la mer septentrionale, d’où à ce qu’on dit, viendrait l’ambre ; j’ignore l’existence d’îles Cassitérides, d’où nous viendrait l’étain. Pour ces îles, j’ai beau donner mes soins à la question, je ne puis entendre dire par personne qui l’ait constaté de ces yeux qu’il existe une mer à ces confins de l’Europe. Mais c’est un fait que l’étain et l’ambre nous viennent d’un bout du monde »
L’ambre venait de la Baltique, là où se jette la Vistule
L’étain (cassiteroz) provenait des îles Britanniques, mais on ne sait pas très bien ce que connaissaient les contemporains d’Hérodote de ces îles
L’étain était très recherché depuis l’antiquité. La métallurgie du bronze fut inventé vers - 3000 bien que l’étain que l’on trouve sous forme SnO2 ne fut pourtant isolé que vers – 1500). (1/6 d’étain + 4/5 cuivre) donne un alliage très dur : bronze utilisé pour la fabrication des essieux de chars, des armes (jambières d’Achille et d’Agamemnon chez Homère), des objets d’art, de la vaisselle (chez les Romains malgré sa toxicité). Sa couleur et sa température de fusion à 230° le rapproche du plomb ce qui explique son nom donné par les phéniciens. L'étain entre dans la composition du bronze des vieux égyptiens. Peut-être ne savaient-ils pas le préparer à l'état isolé. Il n'a été connu à l'état de pureté que plus tard, à l'époque des grecs et des romains.
Iliade, Livre XVIII : "Il dit, et quittant la déesse et se dirige vers ses soufflets… Il jette dans le feu l'airain impénétrable, l'étain, l'or précieux et l'argent; puis il place sur son support une énorme enclume, et prend d'une main un marteau solide et de l'autre sa pince à feu.
"Il fait d'abord un bouclier, grand et fort, qu'il embellit avec art, l'entoure d'un triple cercle dont l'éclat brille et rayonne et y attache une courroie d'argent. Cinq lames forment le bouclier et Vulcain y trace de sa main industrieuse, mille dessins variés. Il y figure le ciel et la mer, le soleil infatigable et la lune en son plein, ainsi que tous les astres dont le ciel se couronne, les Pléiades, les Hyades, la force d’Orion, l’Ourse (à laquelle on donne le nom de Chariot) qui tourne sur place, en observant Orion, et qui seule, ne se baigne jamais dans les eaux de l’Océan"
Et, sur la fin du Livre XVIII: "Une fois fabriqué le bouclier large et fort, il fabrique encore à Achille une cuirasse plus éclatante que la clarté du feu; il fabrique un casque puissant bien adapté à ses tempes, un beau casque ouvragé, qu'il surmonte d'un cimier d'or, il façonne des jambières de souple étain.
3) Polybe
(200-125)
Histoire Livre III C59 vers 160
Polybe dans ses Histoires raconte l’expansion de Rome. Histoires IIIC59 il se contente du silence des négociants marseillais pour traiter de fable les récits de Pythéas
4) Strabon
(64 à 19 avant J.C.)
Livre I p64
Historien grec faisant partie des 1000 otages remis au consul romain Paul Emile après sa victoire à Pydna mettant fin à l’indépendance de la Macédoine
5) Théon
d’Alexandrie (380 avant J.C.)
vers 365 commentateur de l’Almageste de Ptolémée et révision des Eléments d’Euclide
père de la mathématicienne Hypatie
6) Pline
l’Ancien (+24 à +79)
Mort lors de l’éruption du Vésuve Histoire Naturelle
Livre II Cosmologie
Livre IV place une contrée qu’il appelle La celtique sur la mer Baltique
7) Vitruve
(80-0)
Architecte de César et d’Auguste De Architectura Livre 9
Vitruve cite 9/8 à Rome, 4/3 à Athènes, 7/5 à Rhodes,5/3 à Alexandrie
Construit un cadran solaire à Rome
8) Diodore
de Sicile
9) Théon
de Smyrne (2ème siècle après J.C.)
10) Eudème
11) Sextus
Empiricus
Philosophe sceptique du 2ème siècle après J.C.
12) Aëtius
Doxographe du 1er ou 2ème siècle après J.C.
13) Proclus
(entre 400 et 485)
étudie à Alexandrie, dirigeant de l’Ecole d’Athènes
3) Les astronomes arabes
Les sciences arabes naissent à Bagdad avec le calife Al-Mansour (754-775) qui reçut une délégation Indienne en 773 porteuse d’un livre , aussitôt traduit. Un chapitre concernait la trigonométrie et avait une table de sinus à 25 entrées et sinus verse (1-cos).
Leurs sources sont
Siddhanta (VI et VIIième siècle)
Almageste traduit 5 fois
Ouvrages sur la sphère (Ménélaüs, Théodose, Autolycos)
1) al
Battâni Albatagnus (877-929)
le Ptolémée Arabe substitue sinus à corde, donne la formule fondamentale de la trigonométrie sphérique. Il vécut à al Raqq sur l’Euphrate 858-929. « Le Ptolémée arabe » utilise après les indiens, la notion de sinus et non celle de corde et établit la formule fondamentale de la trigonométrie sphérique. Son oeuvre Al Zij traduite en latin et en espagnol fut utilisée par Copernic et Tycho-Brahé
III Timocharis, Hipparque et la
précession des équinoxes
1) Les personnages
Timocharis vécut à Alexandrie vers 300 avant J.C.
Hipparque naquit à Nicée vers -194, s'installa à Rhodes vers -165 où il mourut vers -120.
2) La méthode
Lors d'une éclipse de Lune, on mesure la position d'une étoile par rapport au centre de l'ombre terrestre (milieu de l’éclipse). Connaissant la longitude écliptique du soleil le jour de l'éclipse, donc du centre de l'ombre de la Terre (point diamétralement opposé au soleil), on trouve avec une bonne précision la longitude de l'étoile. On renouvelle les mesures lors d'une autre éclipse pour la même étoile et on compare les longitudes trouvées.
3) L'histoire
On admettra dans la reconstitution historique ci-dessous que les instants des solstices et équinoxes étaient connus à 1/4 jour près, que les clepsydres ou l’observation des étoiles permettaient donnaient l'intervalle de temps depuis le midi à 20mn près, que les angle étaient mesurés à 10’ près. Les années ont été converties dans le calendrier Julien: Hipparque avait, parait-il, reconstitué les dates des éclipses dans son calendrier (grec ou alexandrin) depuis 700 avant J.C.
Observation de Timocharis: "7 jours et 6 heures avant l'instant de l'équinoxe de printemps de l'an -283, j'observais dans la nuit une éclipse de lune. La différence des longitudes entre Spica et la Lune était seulement LSpica- LLune = 0°20’
Observation d'Hipparque: "25 jours après le solstice d'hiver de l'an -132, la mesure de l'angle entre la Lune et Spica, au milieu de l'éclipse, valait LSpica- LLune = +57°30’
La vitesse variable du soleil sur l'écliptique (valeur moyenne 360:365,25=0,985°/jour) était connue des astronomes de l'époque et évaluée à
0 ° 59' 8" = 0,9855° /jour le mois précédant l'équinoxe de printemps
1 ° 3' 44" = 1,0622° /jour le mois suivant le solstice d'hiver
Déterminer avec Hipparque la longitude de Spica en -283 et en -131
En déduire son estimation du déplacement annuel du point g
Calculer la période de la précession en prenant L1950=203,8° et L-50=175,9° pour Spica. Donner L-282 et tracer la trajectoire parcourue par le Pôle Céleste Nord
Retrouver avec un logiciel d'astronomie les éclipses citées ci-dessus, donner les dates juliennes et vérifier les observations ci-dessus.
4) Le point g
à différentes époques
1) Les
Égyptiens
Les pyramides de Khéops, Chephren, Mykérinos construites vers 2500 avant J.C. ne sont décalées par rapport au Nord que de moins de 10'.
Placer le point g sur la Figure 1 et le Pôle Céleste Nord sur la Figure 2 en 2500 avant J.C.
Quelle était « l'Étoile Polaire » à l'époque de la construction de ces pyramides?
2) Homère
llliade Chant XVIII vers 470 à 490: Héphæstos forge pour Achille un bouclier représentant l'univers
"Héphæstos y figure la terre, le ciel et la mer, le soleil infatigable et la pleine Lune, ainsi que tous les astres dont le ciel se couronne, les Pléiades, les Hyades, le baudrier d'Orion, l'Ourse qui tourne sur place en observant Orion et qui seule ne se baigne jamais dans les eaux d'Océan."
Vérifier sur une carte mobile du ciel qu'une partie de l'Ourse peut disparaître sous l'horizon. Justifier néanmoins les vers du poète qui vécut vers 800 avant J.C.
3) Époque
de correspondance entre les "signes..." et les constellations du
zodiaque
Quand le point g se trouvait-il au début de la constellation du bélier, c'est à dire à quelle date le soleil entrait-il dans la constellation du bélier pour l'équinoxe de printemps?
Le soleil entre t-il aujourd'hui dans la constellation du bélier pour l'équinoxe de printemps?
Fig 1: Orbite terrestre et “précession” des Équinoxes
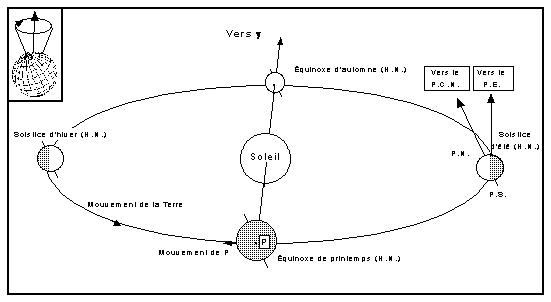
FIG 3: Déplacement de g à travers les constellations
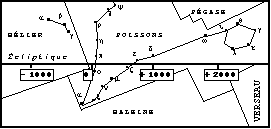
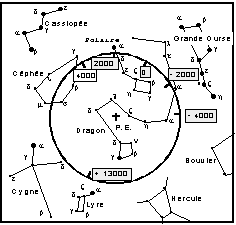
FIG 2: Déplacement du Pôle Céleste Nord (P.C.N.) autour du Pôle de l’Écliptique (P.E.)