Astronomie à l ‘École Élémentaire
I Instructions, niveau, objectifs
II Dans quelles conditions un objet est-il visible?
III Taille et Forme des ombres
IV La propagation de la lumière en ligne droite (source = petite lampe))
VI La réflexion de la lumière.
II Le Plan horizontal - La Verticale
I Programme (Fin Cycle 2 et Cycle 3)
II Surface libre d’un liquide au repos
III Direction de la surface de l’eau au repos
II Premier questionnaire de représentations
II Sur le plan de la classe, de l’École (cycle 1)
III Sur le plan de la localité (cycle 2)
IV Sur la carte de France (cycle 2 et 3)
II Recueil des représentations des enfants
III Observation du paysage et du mouvement du soleil par rapport à l'horizon.
IV Modélisation - Interprétation.
V Observations précises et relevés solaires
VI Le système solaire d’après Copernic.
VII Les observations de Galilée (1564-1642)
VIII Galileo Galilée et les satellites de Jupiter
IX Extrait de « Vie de Galilée » de Bertold Brecht (1939)
XI Sentence du jugement de Galilée.
VI Repérage sur le globe (cycle 3)
II Tracés sur sphère blanche sans axe.
III Lecture et commentaires de planisphères et globes terrestres
IX Heure solaire - Heure légale
II Rappels sur l’heure solaire.
X Le mouvement apparent du soleil par rapport aux étoiles
II Observations (ou étude documentaire)
II Questionnaire de représentations
V Diverses activités concernant la Lune.
I Situation de ces leçons - Pré Requis
II Questionnaire de représentations
V Fabrication et utilisation d’une carte du ciel
VII Résumé: Étoiles et Planètes
|
Chapitre 1 |
Cycle 1: Vivre ensemble, agir dans le monde, découvrir le monde, imaginer, sentir, créer
activités graphiques, repérage dans l’espace
Cycle 2: Observation des effets de la lumière (jeux d’ombre)
Cycle 3: Lumière et ombre
Objectifs:
Démarche scientifique: remettre ses idées en question, se poser des questions, trouver des éléments de réponse (en formulant des hypothèses, avec des expériences ou observations...)
Connaître les caractéristiques d’une ombre: relations avec l’objet, la source lumineuse, la position de “l’écran”
savoir que la lumière se déplace en ligne droite, que l’on peut dévier sa trajectoire par réflexion
savoir qu’un objet peut-être vu s’il “émet” ou s’il “réfléchit” de la lumière
Comportement: structuration de l’espace, prise de conscience du corps, travailler en groupe
Expérience et conclusion: un objet émet ou réfléchit de la lumière
Exercice: Indiquer “émet” ou “réfléchit” la lumière
éclair, papier blanc, ampoule, étoile, abat-jour, flamme, Lune, aiguilles de réveil, ver luisant...
1) fluorescence: le minéral fluorescent émet en visible la lumière ultraviolette ou les rayons X absorbés
Tubes fluorescents: la lumière émise par la vapeur de mercure à l’intérieur du tube est riche en U.V. qui sont transformés par une poudre sur la paroi interne du tube en rayonnement visible.
Matériaux fluorescents naturellement: fluorite, calcite
2) phosphorescence: soumis à un fort éclairage, certains minéraux ré-émettent pendant un moment: gypse
L'ombre de l'Ours Olga Lecaye, École des loisirs La petite girafe Premières Histoires de Popi, Bayard Presse
L'ombre d'Arthur Conte de Gaston Malherbe Ombre mon amie, Album du Père Castor, Flammarion
un des enfants (chat) doit marcher sur l'ombre d'un camarade qui devient Chat
Matériel: petit clou qui sera utilisé pour les relevés d'ombre, Feuille A4 ou A3
la source lumineuse est une lampe de poche ouverte (ainsi, il n'y a pas de réflecteur parasite et la source lumineuse est presque ponctuelle (le filament)
Consigne: on marque un point sur la feuille; où placer la lampe pour que l'extrémité de l'ombre du gnomon touche ce point
on trace une courbe sur la feuille et l'extrémité de l'ombre du gnomon doit suivre la courbe
Conclusion: la taille de l'ombre dépend de la hauteur de la source, la direction de l'ombre dépend de la direction de la source
Comment est l’ombre d’une boule blanche sur un écran? Essayer de joindre la source ponctuelle à l'ombre avec une ficelle
Comment placer trois fiches percées pour apercevoir la tache de la lampe sur un écran?
la lumière se déplace en ligne droite
Discussion avec les enfants
Quelles sont les conditions à remplir pour voir des ombres?
Quelles sont les caractéristiques des ombres?
Dessin: Fais un dessin te représentant avec ton ombre
Relation ombre-objet: formes en relation, ombre et enfant “attachés”, ombre plus grande ou plus petite que l’enfant
Relation ombre-soleil: présence ou non du soleil
Relation ombre - enfant - soleil: on perçoit l’alignement...
On regroupe les dessins et on les affiche par critère
Que pouvons-nous faire pour résoudre les problèmes? aller dans la cour et observer
Premier dessin: On dessine son camarade et son ombre
Retour en classe Réponse aux questions
Dessiner le “trajet” d’un rayon de soleil sur le dessin
Jeux: chat-ombre, ombres chinoises, tracer l’ombre d’un camarade à la craie
Ombres chinoises ou dessiner un profil avec rétroprojecteurs, jeux avec les mains
Observations libres avec le miroir, on joue avec à renvoyer la lumière du soleil, d’une lampe, d’une bougie. Forme de la tâche = Forme du miroir
On éclaire le miroir avec une fente: dessins
On écrit son nom que l’on place devant le miroir: lecture inversée
On dessine plusieurs formes géométriques: symétrie
Déchiffrer un rébus, reconstituer un objet dont seul figure la moitié
Réflexion avec bristol blanc, bristol noir
Qu’est ce qui réfléchit le mieux la lumière?
Ombre propre, portée, zone d’ombre
par groupe de deux enfants et une ampoule de forte puissance placée au centre de la classe
Définir les termes: ombre propre, portée, zone d’ombre Faire dessiner l’expérience
Divers
Avec plusieurs miroirs: deux puis trois
Jeux avec cuillères:
Intérieur de la cuillère: miroir concave, image + petite renversée, en même sens et + grosse si on approche
Extérieur de la cuillère: miroir convexe: image panoramique plus ou moins grande: rétro de voiture
Lampe de poche: forme du miroir Essai avec bougie de renvoyer la chaleur
Décomposition par un prisme
À quoi est due la couleur d’un objet ? Addition des couleurs en peinture
Addition des couleurs avec diapositives
|
Chapitre 2 |
Connaissances: savoir repérer le plan horizontal par la surface d'un liquide au repos, la verticale par la direction du fil à plomb
Concevoir et utiliser des objets techniques mettant en œuvre ces propriétés: niveau, fil à plomb, Comprendre leur intérêt pour des problèmes pratiques (mesures topographiques, mesures de hauteur en astronomie….)
Expérience 1: verser de l’eau dans un récipient:: la surface du liquide en contact avec l’air est appelée surface libre
Expérience 2: viser la surface libre: elle est plane
Expérience 3: l’arête d’une règle s’applique sur la surface libre dans toutes les directions
La verticale: c’est la direction indiquée par le fil à plomb.
Sur une feuille de papier au mur, tracé de la verticale et de sa perpendiculaire avec une équerre
La perpendiculaire au fil à plomb est appelée horizontale
Facultatif: chute des corps suivant la verticale
Suspendre un fil à plomb au-dessus d’une surface libre
À l’aide d’une équerre on vérifie que la surface libre est perpendiculaire au fil à plomb
Conclusion: la surface libre d’un liquide est horizontale
Avec de récipients de formes variées
Les vases communicants: lorsque plusieurs vases communiquent entre eux et contiennent un même liquide, les surfaces libres sont dans le même plan horizontal
Distribution de l’eau
Le niveau d’eau
Les écluses
|
Chapitre 3 |
Cycle 1: Vivre ensemble, agir dans le monde, découvrir le monde, imaginer, sentir, créer
Activités graphiques, repérage dans l’espace
Cycle 2: première découverte de la carte du globe, des éléments du cosmos
Cycle 3: à étudier si cela n’a pas été vu
Connaissance: savoir que la Terre est sphérique, comprendre (pour les cycles 2 et 3) les observations qui ont conduit les hommes à deviner la forme sphérique bien avant que les satellites ne nous la montre
Les enfants expriment souvent verbalement que la Terre est ronde, sans se la représenter dans l’espace sous cette forme ni voir toutes les conséquences sur la position de différents personnages, sur la situation des étoiles, sur la chute d’une pierre, sur ce que veut dire « faire le tour du monde »,...
Un questionnaire approprié permettra à l’enseignant de prendre conscience de ce “faux savoir”, uniquement intellectuel et non assimilé parce que ne faisant pas partie d’une démarche de recherche.
L’essentiel est de comprendre que le “haut” et le “bas” sont des notions locales qui n’ont pas de sens si l’on prend une vue large de la planète. La difficulté sera donc en s’interrogeant sur les observations locales, de passer à un modèle juste du monde qui nous entoure
Diverses questions sur la Terre
Pourquoi ne voit-on pas cette forme de boule si je regarde dehors?
Dans quelle direction faut-il regarder pour voir le centre de la boule?
Qu’y a t-il vers le bas? Dessine-toi sur cette boule. Dessine un ami qui habite très loin, Alger par exemple. Dessine toi et ton ami en train de lancer chacun une pomme en l’air et montre ce qui arrive à cette pomme. Colorie le ciel en bleu
Questions sur la Lune : Quelle est la forme de la Lune? Pour regarder la Lune il faut que je lève la tête, si j’habitais sur la Lune que faudrait-il que je fasse pour voir la Terre?
Donner aux enfants une sphère blanche, placer un horizon (petit cercle de carton), une aiguille ou un personnage Lego
Orienter cette sphère pour que le petit personnage ait le même plan horizontal et la même verticale que nous…
disciple de Platon, environ 350 av JC "Du Ciel II, 14"
Une preuve nous est fournie par l'évidence sensible : sans cette sphéricité, les éclipses de Lune ne présenteraient pas les segments tels que nous les voyons. C'est un fait que si, dans les aspects qu'elle offre chaque mois, la Lune revêt toutes les variétés (puisqu'elle devient droite, bombée et concave ; dans les éclipses, la ligne qui la limite est toujours une ligne courbe, de sorte que, s'il est vrai que l'éclipse est due à l'interposition de la Terre, c'est la forme de la surface de la Terre qui, étant sphérique, sera la cause de la forme de cette ligne.
En outre, nos observations des astres montrent avec évidence, non seulement que la Terre est circulaire, mais que c'est un cercle qui n'est pas d'une grandeur considérable. En effet, il suffit que nous nous déplacions tant soit peu vers le Sud ou vers le Nord, pour amener une évidente modification du cercle de l'horizon, de sorte que les étoiles qui sont au-dessus de nos têtes sont tout à fait changées, et n'apparaissent plus les mêmes si nous nous déplaçons vers le Nord ou vers le Sud En effet, il y a des étoiles qu'on voit en Égypte et dans le voisinage de Chypre, et qu'on n'aperçoit pas dans Les régions situées au Nord ; et les étoiles qui, dans la région du Nord, n'échappent jamais à notre champ visuel, ont leur coucher dans les régions du Sud. Il résulte évidemment de ces faits que non seulement la forme de la Terre est circulaire, mais encore qu'elle est une sphère qui n'est pas très grande, car autrement l'effet d'un si faible changement de position ne serait pas si vite apparent. C'est pourquoi ceux qui croient qu'il y a continuité de la région avoisinant les Colonnes d'Hercule et de la région de l'Inde, et que, de cette façon, il n'y a qu'une seule mer, ne semblent pas professer une opinion tellement incroyable. Ils en donnent encore comme preuve le cas des éléphants, dont l'espèce se rencontre dans chacune de ces régions extrêmes, ce qui tend à faire croire que c'est en raison de leur continuité que les régions extrêmes sont affectées des mêmes caractéristiques.
(extrait de la revue "Espace Information n°31 octobre 1985).
Ce 21 juin, un homme accroupi au centre de la grande glace d'Alexandrie, un misérable cadran solaire à la main, se propose de mesurer les dimensions du globe terrestre.
Calculer la taille exacte du monde quel rêve merveilleux, quelle arrogante ambition de la créature microscopique vivant sur la surface immense de la planète ! Et, hélas ! quelle entreprise futile. ...........
A midi juste, en ce jour du solstice d'été, il va essayer de déterminer avec précision la grandeur du globe terrestre à l'aide d'un simple gnomon. Cet instrument peu élaboré ne pourra que lui donner l'angle sous lequel un objet vertical projette son ombre. Mais pour réaliser son dessein, Ératosthène compte surtout sur la richesse des renseignements qu'il a puisés dans la bibliothèque.
Une information amusante, mais sans aucune valeur scientifique apparente, doit servir de base à la méthode aussi simple qu'ingénieuse qu'Ératosthène a maintenant l'intention d'employer pour prendre la mesure de la Terre. II a lu quelque part que dans la Ville de Syène (aujourd'hui Assouan), où il n'est jamais allé, le Soleil de midi, le jour du solstice, est absolument perpendiculaire
et ne projette aucune ombre. Des voyageurs rapportaient qu'à ce moment précis, on pouvait en regardant dans un puits très profond et étroit, y voir le Soleil se réfléchir d'aplomb. Tel n'était pas le cas à Alexandrie : même à midi, même un jour de solstice les rayons solaires n'étaient pas parfaitement verticaux.
Ératosthène était de ces savants de l'antiquité qui croyaient déjà que la Terre est une sphère. Cette théorie n'était pas universellement reconnue, loin de là. Ses adversaires avaient pour eux l'évidence quotidienne, ce que voient nos yeux, et les esprits scientifiques étaient entraînés à n'accepter comme vérité que ce qu'ils voyaient, la vérité telle que l'œil la perçoit étant indiscutablement que la Terre est plate.
Il y avait bien, naturellement, des phénomènes difficiles à concilier avec l'idée d'un monde plat ainsi l'apparition, à l'horizon, d'un navire dont on ne voit d'abord que le haut du mât, puis la voilure et enfin la coque. Certains philosophes en déduisaient une preuve de la courbure de la Terre, mais ils demeuraient une minorité.
|
Chapitre 4 |
Cycle 1: Plan de la classe (meubles, place des enfants, tableau, bureau) ou de l’école
Cycle 2: Première découverte de la carte du quartier, du globe, des éléments du cosmos
Cycle 3: Géographie: regard sur le monde, Sciences Physiques: points cardinaux et boussole
Démarche: apprendre à s’orienter dans l’École, dans la ville, avec une carte
Connaissances
La direction du Nord est celle qui nous conduit à un point particulier de la Terre « Le pôle Nord », dont on précisera la définition après avoir vu le jour et la nuit
Les “points cardinaux” sont des directions liées à un lieu et définies à partir du nord
Méthodes
Savoir passer de la maquette au monde réel, du monde réel à la maquette
Travail inter-disciplinaire: Français, histoire, géographie...
Travail d’équipe: utilisation de cartes, faire des relevés de direction du vent
Échelle, couleurs, bâtiments publics, quadrillage. À quoi set le quadrillage? Réponse: à se repérer...
* Lieu donné, trouver son code * Code donné, trouver le lieu
Expliquer Vent du Nord ... puis faire de la météo
En France placer les vents: Mistral, Tramontane, Vent d’Autan
Mythologie grecque: Éole et ses fils (Borée, le vent du Nord, Aquilon, Zéphyr, Euros)
Étudier un plan de cathédrale: par exemple primatiale Saint-Jean
(éventuellement sinon le sujet sera traité au cycle 3 avec le repérage sur le globe)
Que veulent dire les lettres N, S, E, O Que représentent-elles lorsque l’on se trouve à Lyon:
Le Nord: la direction du Pôle Nord : point par lequel passe l’axe de rotation de la Terre (pas encore introduit)
le Sud: la direction du Pôle Sud
l’Est et l’Ouest: directions placées à angle droit des précédentes
Construction d’une rose des vents: Division du cercle en 8 et construction graphique
Donner une carte ancienne de Lyon et une carte actuelle
Rédiger quelques lignes sur l’extension de la ville
Fonctions de la ville
Observation minutieuse du plan
Dresser les éléments observés et comparer avec la liste suivante
Hotel de Ville, gare, cimetière, musée, parking, jardin, places, rues
Classer par rubrique: Transport, Culture, Religion, Loisirs, Administration
Quelle fonction de la ville ne figure pas: commerce, marché, gare
Différents développement des villes
En étoile (Munich, Lyon), en cercles concentriques (Paris, Milan ...), en ligne (La Haye , Montluel ...)
Imaginer votre ville idéale
Que sera pour vous une ville du futur? ou Imaginez votre ville idéale.
Création d’une ville imaginaire en maquette
Partir de la cour de l’Hôtel de Ville
Qu’est-ce que l’Hôtel de Ville?
Quel objet observes-tu sur un des murs? Quelle est l’orientation de ce mur? Pourquoi cet objet est-il placé sur ce mur?
Prendre la rue Joseph Serlin pour aller Place des Terreaux
Quel est le bâtiment que tu observes et que voit-on sur la place?
Prendre la rue Constantine puis le Pont La Feuillée. Quelle est la rivière traversée?
Quel est le bâtiment qui se trouve sur la place en face du pont?
Prendre la rue Juiverie à gauche de ce bâtiment
Faire le tour du bâtiment par la Rue des loges puis la rue Soufflot
Quel est la fonction actuelle de ce bâtiment et quelle était l’ancienne?
Quel est le musée qui se trouve de l’autre côté?
Prendre la Rue de la Fronde pour aller place du Gouvernement
Trabouler au n°. Sur quel quai arrivons nous?
Trabouler au n°
Prendre la Rue Saint Jean au n° Trabouler au n°
Dans quelle rue arrivons-nous?
Prendre la rue de La Bombarde jusqu’à l’esplanade ave des vestiges
Arrête toi un moment pour écouter les explications
Prendre la Rue Saint Étienne pour arriver Place Saint Jean
Quel est le grand bâtiment qui se trouve sur la place? Horloge astronomique…
Afficher au tableau deux cartes de la région lyonnaise (par exemple 1/50 000 et 1/100 000)
Noter l’échelle 1/50 000: les dimensions réelles sont 50 000 fois plus grandes que sur la carte:
1cm sur la carte représente 50 000cm=0,5km en réalité
Lecture d’une photo de paysage et utilisation de la carte 1/25 000 de Lyon Dans quelle direction sont prises les photos? Quelles différences entre chacune? Découper le paysage en différents plans en partant de l’observateur Décrire le paysage plan par plan? Plan1: Plan2: Plan 3:
Quelle est la tour ronde que l’on aperçoit sur l’une des photos à l’extrême droite? Où se trouve le pont de l’autoroute?
À quelle distance se trouve la tour? Quelle heure est-il? Reconnaissez-vous des villages ou des bâtiments?
Exercice1: Tu disposes des cartes suivantes
*Planisphère *Europe *France *Savoie Dauphiné *Lyon-Grenoble
*Grand Lyon *Lyon * Domaine de La Croix Laval
Choisis pour chacune l’échelle parmi celles proposées
¼ 500 000: 1/100 000 000: 1/1 000 000: 1/50 000:
1/250 000: 1/100 000: 1/7 500: 1/25 000:
Chercher les distances
Lyon à Grenoble Lyon à Berlin Lyon à Montluel Lyon à Vancouver?
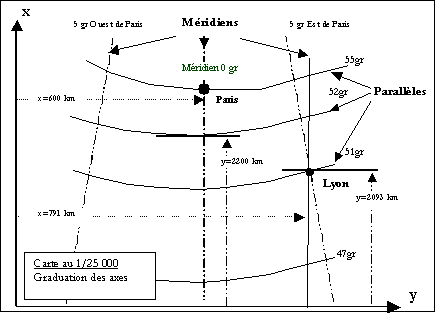
Projection de Lambert : sur un cône sécant à la Terre:
les méridiens se projettent en des droites concourantes et les parallèles en des arcs de cercle
Lambert I (Nord 55gr), Lambert II (Centre 52gr), Lambert III (Sud 49gr), Lambert IV (Corse 46gr)
Latitude et longitude
en ° par rapport au méridien de Greenwich et l’équateur, en gr par rapport au méridien de Paris et l’équateur
Amorces kilométriques bleues intérieures
horizontales: origine au méridien de Paris décalé de 600km
verticales: origine au parallèle de tangence (52 gr pour Lambert II) décalé de 2200km
Amorces kilométriques noires extérieures
horizontales: origine au méridien de Greenwich verticales: origine à l’équateur

|
Chapitre 5 |
Cycle 1: Vivre ensemble, agir dans le monde, découvrir le monde, imaginer, sentir, créer, activités graphiques
Cycle 2: Première découverte du globe, des éléments du cosmos. Le temps dans la vie des hommes
Cycle 3: *"Mouvement apparent du soleil", *Rotation de la Terre sur elle-même et conséquences *Points cardinaux et boussole
saisir rapidement l'enjeu de l'échange et en retenir les informations successives,
questionner l'adulte ou les autres élèves à bon escient,
se servir de sa mémoire pour conserver le fil de la conversation et attendre son tour, s'insérer dans la conversation,
reformuler l'intervention d'un autre élève ou du maître.
commencer à prendre en compte les points de vue des autres membres du groupe,
commencer à se servir du dialogue pour organiser les productions du groupe,
commencer à rapporter devant la classe (avec ou sans l'aide de l'écrit) de manière à rendre ces productions compréhensibles.
|
Sciences expérimentales et Technologie |
Parler |
Lire |
Écrire |
|
utiliser le lexique spécifique des Sciences dans les différentes situations didactiques mises en jeu |
lire et comprendre un ouvrage documentaire, de niveau adapté, portant sur l'un des thèmes au programme |
prendre des notes lors d'une observation, d'une expérience, d'une enquête, d'une visite |
|
|
formuler des questions pertinentes |
trouver sur la toile des informations scientifiques simples, les apprécier de manière critique et les comprendre |
rédiger, avec l'aide du maître, un compte rendu d'expérience ou d'observation (texte à statut scientifique) |
|
|
participer activement à un débat argumenté pour élaborer des connaissances scientifiques en en respectant les contraintes (raisonnement rigoureux, examen critique des faits constatés, précision des formulations, etc.) |
traiter une information complexe comprenant du texte, des images, des schémas, des tableaux, etc… |
rédiger un texte pour communiquer des connaissances (texte à statut documentaire) |
|
|
utiliser à bon escient les connecteurs logiques dans le cadre d'un raisonnement rigoureux |
La pratique des outils des arts visuels, dessiner, photographier, filmer, faire des maquettes permet à l'élève de développer la perception de son environnement paysager et architectural. Il doit apprendre à mieux percevoir les limites, les oppositions entre formes et fonds, les relations et les proportions, la lumière et les ombres, la structure et l'ensemble.
poser des questions précises et cohérentes à propos d'une situation d'observation ou d'expérience,
imaginer, avec l'aide du maître, un dispositif expérimental susceptible de répondre aux questions que l'on se pose
participer à la construction d'un dispositif expérimental ou d'observation, observer avec ou sans instruments, mesurer,
rechercher des documents sur un thème donné dans la BCD ou sur la toile,
participer à la préparation d'une enquête ou d'une visite en élaborant un protocole d'observation ou un questionnaire,
évaluer la validité des observations réalisées et les confronter aux savoirs établis que l'on a trouvés dans la documentation,
rédiger, avec l'aide du maître, un compte rendu d'expérience ou d'observation (texte à statut scientifique),
rédiger un texte pour communiquer des connaissances (texte à statut documentaire)
Avoir compris et retenu « course du soleil » durant la journée, variation de durée des jours et des nuits, évolution au cours des saisons (calendrier), lien avec la boussole et les points cardinaux; un petit nombre de modèles simples concernant ces phénomènes, le système solaire et l'univers
Être capable de trouver le sens de rotation de la terre sur elle même en ayant observé le mouvement du soleil par rapport à l'horizon
Comparer des représentations globales de la Terre (globe, planisphères...) et du monde (cartes, images d'artistes ou publicités. ..)
Être capable de mettre en relation des cartes à différentes échelles pour localiser un phénomène, de réaliser un croquis spatial simple
Un recueil de représentations permet aux enfants d’exprimer leur représentation du monde, à l’enseignant d’en prendre connaissance. Il leur permet aussi de s'approprier un problème qui ne les concernait pas au départ, au moyen de leur imaginaire, de leur goût pour le dessin, la peinture, l'écriture….
Les enfants expriment souvent leurs connaissances livresques par des phrases justes mais des dessins faux. En ce qui concerne la succession des jours et des nuits ou des saisons, on constate souvent que même connaissant le modèle héliocentrique ils sont ignorants de ce que perçoit un observateur terrestre et qu’ils n’ont pas une représentation spatiale juste du phénomène. Seule une lente progression (basée d’abord sur l’observation, ensuite sur une modélisation des phénomènes à l’aide d’une maquette en trois dimensions, enfin sur une étude documentaire) pourra faire évoluer leurs représentations.
Il s'agit de poser des questions qui induisent le moins possible une réponse donnée: la
question posée pourrait-être:
Pourquoi y a t-il des jours et des nuits? Explique pourquoi il y a alternance de jour et des nuit?
Fais un dessin (ou schéma légendé) et une phrase de texte explicatif.
La question ci-dessus n'est pas si neutre qu'elle paraît (on aurait pu demander: "Où est le soleil pendant la nuit?" et induire d'autres réponses. A l'enseignant de choisir. L'essentiel est d'engager un questionnement qui devrait germer quel que soit la formulation de la question de départ). Question plus neutre, mais plus floue: "Dessine le monde avec les astres que tu connais et ce qui s'y passe…"
"La nuit cache le soleil." "La lune cache le soleil." "Les nuages
cachent le soleil de plus en plus , sa devien nuit et on dort".
"La journée il y a le soleil donc il fait jour, la nuit il y a la lune donc il fait nuit."
"Pour dormir" "Parce que s'il n'y avait pas de jour, on ne pourrait pas sortir dehors, parce qu'il ferait trop noir; et si il n'y aurait pas de nuit, on ne pourrait pas dormir"
"Quand c'est la nuit le soleil c'éloigne de la Terre"
"Parce que la Terre tourne autour du soleil". "C'est à cause du sitème soleire. La terre tourne autour du soleil."
(Modèle expliquant l'alternance jour-nuit par la révolution de la Terre autour du soleil)
"Le soleil tourne autour de la Terre…""Quand le soleil tourne, en France il fait jour et au Brésil il fait nuit. Sa fait chacun son tour."
"Quand la Terre tourne, le soleil ne bouge pas. La terre s'éclaire morceau par morceau parce que la Terre tourne et le soleil éclaire la partie qui est devant lui."
III Observation du paysage et du mouvement du soleil par rapport à l'horizon
L'observation, l'étude, la représentation d'un paysage est une activité reliant bien des disciplines (géographie, nature et environnement, Sciences-Physiques, Arts plastiques) et des compétences des enfants (observation, imaginaire, habileté graphique…)
Sans s'occuper du soleil elle peut constituer par elle même une activité intéressante un jour nuageux (ou non)
Par une telle étude progressive, l’enfant prend conscience d’abord de son environnement puis des phénomènes qui s’y produisent.
L’enseignant fait d’abord le tour du paysage avec les enfants en leur demandant les éléments remarquables: obstacles naturels, lointains si possible, (montagnes, lacs, rivières...), constructions (immeubles, maisons, usines, cheminées...), végétation (arbres, forêts, champs..), maison de l'enfant…
L'observation directe du soleil peut entraîner des brûlures irrémédiables de la rétine…
feuille A3 sur support cartonné: crayon de papier (et/ou crayons de couleur)
Les enfants doivent tendre un bras à gauche, un bras à droite: sur environ 180° représenter sur la feuille de format A3 les éléments du paysage, en particulier "le fond lointain avec des éléments remarquables (tour, sommet, arbre …)
Pour un enfant ayant choisi une orientation donné: sur ton dessin il faudra cet élément à gauche de ta feuille correspondant à ce que désigne ton bras gauche, cet élément à droite que désigne ton bras droit (sinon les enfant commencent par dessiner ce qui est devant eux et n'ont pas une feuille assez large pour respecter la consigne du panorama à 180°)
Il faudra ensuite placer le soleil au dessus de son point de repère
Avec les bras ressentir physiquement la hauteur du soleil par rapport à l'horizon (un bras horizontal, l'autre en direction du soleil)
Demander au dessus de quel repère se trouve le soleil (on ne regarde pas le soleil!). En est-il toujours ainsi …
Sur votre dessin dessiner en pointillés un rond indiquant la position présumée du soleil au milieu de la journée et le soir (ou coller trois gommettes de couleurs différentes)
On revient au milieu de journée: vers 13h30 en "horaire d'été" et vers 12h30 en "horaire d'hiver" (dernier dimanche d'octobre au dernier samedi de mars)
On dessine le soleil avec trois couleurs différentes à 8h45, à mi-di et à 16h15. Chaque enfant observe la position du soleil et avec un feutre de la même couleur que ses gommettes, il rectifie les prévisions qu’il avait faites sur son dessin
Chaque enfant compare son panorama prévisionnel fait en classe et les rectifications faites lors des observations.
Débat: le soleil est-il toujours au même endroit pendant la journée? Qu’est-ce qui a changé? Tout le monde est-il d’accord sur la hauteur du soleil? L’avons nous vu au zénith?
Le soleil a un mouvement relatif pendant la journée: il “apparaît” du côté de … (Alpes ou …), est haut par rapport à l’horizon en milieu de journée et “disparaît” du côté du Massif Central. (Les repères géographiques remarquables et lointains ont été choisis pour Lyon; ce serait dommage d'introduire maintenant les points cardinaux en disant que le soleil "apparaît vers l'est car le but de ces séquences est précisément de comprendre ce que représentent le nord, le méridien Nord-Sud puis de définir ensuite localement l'est et l'ouest et d'introduire la Rose des Vents…
Qu’est-ce que l’on pourrait faire pour essayer de comprendre ce que nous avons observé ainsi que les explications que vous avez données à propos de l'alternance Jour-Nuit… Utiliser les boules blanches en polystyrène (sans axe)
Modéliser les explications des enfants (géocentrisme et héliocentrisme)
Comment choisir entre les deux hypothèses? Réponse: Nous n’avons pas les moyens de décider et seule une étude documentaire pourra nous aider (Conception des Égyptiens, des Chinois, des Grecs, Vie de Copernic et Galilée par exemple, Vidéos).
Résumé possible (en élaborer un collectivement) : nous n'avons pas pu avec notre modélisation et nos observations choisir entre le modèle de Copernic (héliocentrique) et celui de Ptolémée (géocentrique). Des observations et des expériences (par exemple parallaxe des étoiles) montrent pourtant que c'est le modèle de Copernic qui est celui correspondant à la réalité: la Terre tourne sur elle même (jour) et autour du soleil (365,25 jours)
Résumé pour l'enseignant: Les hommes n’ont réellement compris que depuis 400 ans que le mouvement du soleil et de la voûte céleste qu'ils observaient par rapport au paysage était lié au choix (bien naturel) d’un repère terrestre. Les mouvements des astres sont en fait bien plus simples à étudier dans un repère lié aux "étoiles" et les lois physiques ne s'expriment simplement que dans un tel repère. Par rapport à ce repère (Soleil au centre et axes liés aux étoiles) la Terre tourne sur elle-même: ce mouvement explique la succession des jours et des nuits, le mouvement par rapport à notre horizon du soleil la journée, des étoiles la nuit.
On appellera jour la période de rotation de la Terre sur elle-même. La Terre tourne de plus autour du soleil en 365 jours ¼
Les hommes ont décidé de diviser le jour en 24 parties égales qu'ils ont appelées les heures.
Puisqu'on a décidé de choisir le modèle où la Terre tourne sur son axe on peut donner à chaque enfant une brochette qui le matérialise et permet de la faire tourner. Chaque enfant doit trouver sur sa boule: Soleil apparaît, le "Milieu du jour (mi-di solaire)", Soleil disparaît, le "Milieu de nuit" (mi-nuit)
Si on a fait la leçon sur le repérage à la surface de la Terre (Chapitre suivant) ou si l'on dispose de petites Terres sur lesquelles sont indiqués les pays et continents: Dans quel sens faire tourner la Terre sur elle-même, le soleil étant positionné?
Définitions: Nous appellerons “jour” la durée séparant deux mi-dis solaires, “journée” la période séparant le lever du coucher du soleil, “nuit” la période séparant le coucher du lever du soleil
Constater avec les enfants que d'un dessin à l’autre il y a des variations de hauteur du
soleil sur les représentations du paysage.
Est-il possible de faire une mesure de hauteur du soleil qui mettrait tout le monde d’accord?
Il existe de vieux appareils (bâton de Jacob, quadrant de Copernic...) qui permettent de mesurer l’angle, mais la plus vieille méthode est le relevé d’ombre avec un bâton vertical (gnomon signifiant indicateur en grec). Faire un relevé dans la cour toutes les heures
On indique l’heure de chaque relevé. L’enseignant marque les ombres au coucher du soleil. Il les couvrira si possible d’une feuille de plastique pour les protéger jusqu’au lendemain s’il est possible de les laisser sur place
Matériel: lampe de poche, boule blanche et une aiguille plantée à Lyon
L’enseignant: J’aimerais voir comment sont les ombres le matin, au "milieu de la journée", le soir
Nous ferons à partir de maintenant tourner la Terre sur un axe que l’on appellera l’axes des pôles. Faire traverser les sphères avec une brochette et marquer Pôle Nord et Pôle Sud
Comment est l’ombre au milieu du jour? Réponse: elle est la plus courte et indique le Pôle Nord.
Que peut-on en tirer? Réponse: On peut tracer la direction du Nord dans la cour
Examen des relevés. Est-ce que cela coïncide avec nos prévisions?
Peut-on tracer la direction du pôle Nord? Réponse: Oui, c’est la direction de l’ombre la plus courte
Aller dans la cour à midi solaire (avec le calendrier musulman, le calendrier du Père Benoît des jardiniers, les éphémérides du journal local qui donnent l’heure du lever et du coucher du soleil… ) et tracer l’ombre à cet instant
On colle à partir de 8h30 toutes les heures une gommette, de façon que l'ombre de la gommette tombe au centre de la sphère du saladier (avec un tout petit personnage, on peut dire: le rayon de soleil aboutit dans l'œil de l'observateur et on repère le mouvement du soleil sur la voûte céleste par rapport au paysage)
· Le soleil a un mouvement régulier contenu dans un plan incliné par rapport au paysage (on peut mesurer cet angle: environ 44° à Lyon)
· Le soleil tourne régulièrement autour d’un axe incliné par rapport à l'horizon (on peut mesurer ce deuxième angle: environ 46° à Lyon)
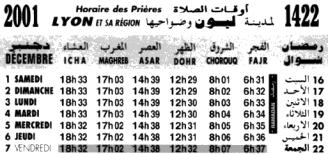
Pour la ville de Lyon, on lit de droite à gauche, en heure légale en France
FAJR : aube ; ici 1h30 avant le lever mais en principe horaire calculé avec le soleil à -18° sous l’horizon
CHOROUQ : lever du soleil
DHOR : midi solaire ; le soleil se trouve au sud et culmine
ASAR : l’ombre du gnomon est égale à la longueur de son ombre à midi plus sa hauteur (1er Asr)
MAGHREB : coucher du soleil
ICHA : crépuscule ; ici 1h30 après le coucher mais en principe …
Copernic écrit dans « de revolutionibus », au sujet des révolutions (des planètes)
" Toutefois les orbites du Soleil, de la Lune et des planètes doivent être circulaires ou composées d'un ensemble de mouvements circulaires, car leurs variations sont régies par des lois immuables dont dépend leur périodicité. Si ces orbites n'étaient pas circulaires elles ne pourraient tout simplement pas exister, car seul le cercle permet de reproduire exactement une situation passée. . .
C'est dans un texte de Cicéron que j'ai rencontré pour la première fois l'hypothèse de Nicète selon laquelle la Terre tournait. Plus tard, en lisant Plutarque, j'ai découvert qu'il partageait cet avis; par conséquent j'ai, moi aussi, commencé à méditer sur la rotation de la Terre. Comme de nombreux savants avaient pris la liberté d'utiliser autant de cercles qu'il leur semblait nécessaire pour expliquer les phénomènes célestes, j'ai pensé pouvoir présenter sans difficulté une démonstration des mouvements planétaires aussi plausible que celle de mes prédécesseurs, en partant du fait que la Terre tournait, bien que cette idée semblât absurde de prime abord . . . "
……
" Les idées exposées ci-dessous sont difficiles, voire impossibles à admettre; elles entrent en contradiction avec les conceptions courantes. Malgré tout, et avec l'aide de Dieu, nous allons rendre toute chose claire du moins pour les mathématiciens. . .
La première sphère, la plus éloignée du Soleil, porte les étoiles fixes. Elle englobe toutes les autres sphères. Elle est immobile et c'est la partie de l'univers la mieux indiquée pour servir de référence aux déplacements et aux positions des autres "célestes". Si certains pensent encore que cette sphère est mobile, nous sommes dès maintenant en désaccord… En allant de la sphère des étoiles fixes vers le Soleil, nous trouvons d'abord Saturne dont la révolution dure trente ans, puis Jupiter qui parcourt son orbite en douze années, ensuite c'est le tour de Mars dont la rotation dure deux ans. La quatrième sphère porte la Terre et la Lune (révolution d'un an), en cinquième position il y a Vénus (révolution de 9 mois), la sixième et dernière orbite étant celle de Mercure (révolution de 80 jours). Le Soleil se tient immobile au centre de l'ensemble
Ce que prévoit le modèle de Ptolémée 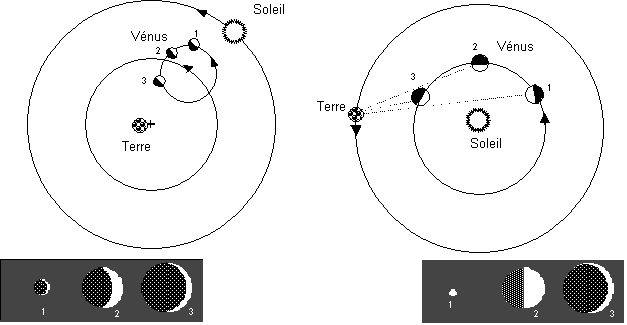
Ce que voit Galilée
Galilée dessine son relief; il calcule même la hauteur des montagnes d’après la taille des ombres
Il n’est pas “parfait”, il possède des tâches, qui apparaissent, se resserrent en s’approchant du bord puis disparaissent: elles ne sont donc pas dues à des défauts de la lunette, le soleil tourne sur lui-même.
la lunette lui permet de séparer les milliers d’étoiles qui la compose
Galilée croit voir une planète triple avec ses observations de 1610, 1612 (“les deux planètes supplémentaires ont disparu), 1616 (“les deux planètes reviennent mais plus minces”). En 1655 Huygens identifie les anneaux et donne l’explication correcte: Saturne est vue, depuis la Terre, sous un angle variable lorsqu’elle se déplace autour du soleil.
![]()
Galilée est né à Pise, en Italie. Il enseigna les mathématiques à Padoue puis à Florence.
En cette année 1609 il prend connaissance d’une nouvelle invention d’un opticien hollandais utilisant deux lentilles de verre. Judicieusement choisies et disposées de part et d’autre d’un long tube, celles-ci forment un instrument qui rapproche les objets observés! Les premières lunettes sont médiocres, ne grossissent que deux ou trois fois et déforment les objets. Mais Galilée en fabrique une grossissant huit fois avec un objectif de 4 cm, qu’il présente le 25 août 1609 au doge de Venise lui permettant de voir à l’avance les bateaux arrivant au port. Il perfectionne la taille et la qualité des verres pour disposer finalement le 7 janvier 1610 d’une lunette grossissant trente fois qu’il dirige vers le ciel. Cette nuit-là il observe Jupiter, qui apparaît comme une toute petite sphère et découvre à côté trois points brillants, deux vers l’est, un à l’ouest, alignés avec Jupiter. La nuit suivante les trois points se sont déplacés autour de Jupiter; les trois sont à l’ouest. Ce ne sont donc pas des étoiles, ce sont des compagnons de Jupiter, des satellites. Les nuits suivantes, la ronde se poursuit et un quatrième satellite se dévoile même dans le champ de la lunette! Les adversaires de Copernic affirmaient que si la Terre tournait autour du soleil, la lune ne pourrait la suivre dans sa course. Cet argument ne tient donc pas: une planète peut tourner autour d’un astre et entraîner avec elle des satellites.
Les découvertes de Galilée ne s’arrêtent pas là. Il observe ensuite les montagnes lunaires dont il évalue la hauteur en mesurant la longueur de leurs ombres, les taches solaires et leurs déplacements: ce qui est au-delà de la lune est aussi en évolution, comme sur Terre. Les phases de la planète Vénus (croissant, Vénus « pleine » ...) distinguées grâce à la lunette permettent d’affirmer que Vénus tourne autour du Soleil et non autour de la Terre.
Les observations de Galilée ne sont pourtant pas décisives pour passer au modèle héliocentrique de Copernic.
1) Quels sont les problèmes techniques posés par la réalisation de la lunette?
3) Pourquoi les trois points brillants découverts ne sont-ils pas de simples étoiles?
4) Dessine les observations de Galilée le 7 et le 8 janvier 1610, en plaçant trois * représentant les trois premiers satellites découverts?
![]() 7 janvier 1610
7 janvier 1610
![]() 8 janvier 1610
8 janvier 1610
5) Énumère les autres observations de Galilée, en les expliquant.
6) Celles-ci prouvent-elles que la Terre tourne sur elle-même et se déplace autour du soleil?
Dialogue entre Galilée et Andrea, le fils de sa gouvernante . Nous sommes en 1609 à Padoue.
GALILÉE: Ce que je t’ai dit hier, l’as-tu compris depuis ?
ANDREA: Quoi? L’histoire de Copernic avec la rotation?
GALILÉE: Oui.
ANDREA: Non. Pourquoi voulez-vous que je comprenne? C’est très difficile et je vais avoir seulement onze ans en octobre.
GALILÉE: Justement, je veux que toi aussi tu le comprennes. C’est pour ça, pour qu’on le comprenne, que je travaille et que j’achète ces livres coûteux au lieu de payer le laitier.
ANDREA: Mais je le vois, que le Soleil, le soir, s’arrête ailleurs que le matin. Avec ça, il ne peut pas être immobile! Jamais de la vie.
GALILÉE: Tu vois ! Qu’est-ce que tu vois? Tu ne vois rien du tout. Tu écarquilles les yeux, c’est tout. Écarquiller n’est pas voir. (Il pose le trépied en fer au milieu de la chambre.) Ceci est le Soleil, donc. Assieds-toi. (Andrea s’assied sur une des chaises, Galilée est debout derrière lui.) Où est le Soleil, à droite ou à gauche ?
ANDREA: À gauche.
GALILÉE: Et comment ira-t-il à droite ?
ANDREA: Si vous le transportez à droite, naturellement.
GALILÉE: Seulement de cette manière ? (Il soulève Andrea avec la chaise et accomplit avec lui une demi-rotation.) Où est maintenant le Soleil ?
ANDREA: À droite.
GALILÉE: Et il a bougé ?
ANDREA: Ça non.
GALILÉE: Qu’est-ce qui a bougé?
ANDREA: Moi.
GALILÉE (hurle): Faux ! Idiot ! La chaise!
ANDREA: Mais moi avec elle!
GALILÉE: Évidemment. La chaise, c’est la Terre. Tu es assis dessus.
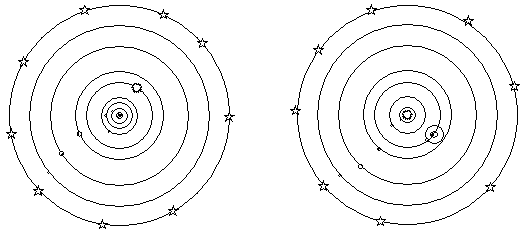
Modèle de Ptolémée (90-158) Modèle de Copernic (1473-1544)
Ptolémée: Terre, immobile, autour de laquelle tournent Lune, Mercure, Vénus, Soleil, Mars, Jupiter, Saturne, Sphère des étoiles
Copernic: Soleil, immobile; tournent autour sur des cercles: Mercure, Vénus, Terre et Lune, Mars, Jupiter, Saturne, Sphère des étoiles
Kepler (1571-1630) montra quelques années plus tard que les orbites des planètes étaient des ellipses
À première vue, il paraît naturel de choisir un système de référence lié à la Terre pour repérer les mouvements.
D’ailleurs sur de courtes durées, on peut comparer l’observateur terrestre au conducteur d’une automobile roulant en ligne droite à vitesse constante : tout se passe dans le véhicule comme si il était au repos.
Mais les phénomènes d’une durée supérieure à ceux que nous observons habituellement montrent que la Terre n’est pas un repère « galiléen » dans lequel les lois qui régissent les mouvements prennent une forme simple.
La « dynamique » qui étudie ces mouvements est abordée à partir du Lycée et sort du champ de l’Ecole Primaire.
1) Aristarque, vers 250 avant J.C., présumait déjà que la Terre tournait autour du soleil car ses observations l’avait conduit à le trouver très grand par rapport à celle-ci.
2) Newton vers 1686, publie les « Principia », synthèse expliquant les mouvements des astres dans le ciel et des corps sur la Terre par une même théorie : la « gravitation universelle »
« Je suis monté sur les épaules de géants » (Nicolas Copernic, Tycho Brahe, Galiléo Galiléi, Jean Kepler)
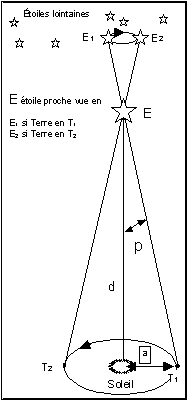 3) La parallaxe
annuelle mesurée par Friedrich Bessel en 1838.
3) La parallaxe
annuelle mesurée par Friedrich Bessel en 1838.
Le dessin ci-contre montre l’angle de parallaxe p qui dépend de la distance d et de la direction de l’étoile observée.
Cet angle est extrêmement faible (p=0,76” d’arc pour l’étoile la plus proche, Proxima du Centaure) : il ne pouvait-être mesuré à l’époque de Copernic.
Le satellite Hipparcos mesure la position, le mouvement propre et la parallaxe des étoiles avec une précision de 0,002”
20”: pièce de 10 Francs à 240 m
1”: pièce de 10 Francs à 4,7 km
0,001”= pièce de 10 Francs à 4 700 km
On peut utiliser la méthode photographique : un champ stellaire est photographié au foyer d'une lunette de grande focale (f=10mètres par exemple), une vingtaine de fois par an.. L'étoile proche se déplace d'environ 10 microns sur la plaque

4) L’aberration de la lumière trouvée et expliquée en 1726 par James Bradley qui cherchait à mesurer l’effet précédent.
La direction de la lumière d’une étoile donnée semble changer suivant la vitesse (et donc la position) de la Terre sur sa trajectoire. Le phénomène est analogue à la direction apparente de la pluie qui semble changer lorsqu’on change de direction.
Les étoiles semblent décrire une ellipse de demi-grand axe 40’’
(Valeur correspondant à Vterre=30km/s et Vlumière=300 000km/s)
5) le pendule conçu et réalisé par Léon Foucault en 1851 avec une masse de 28 kg attachée à 68 m de fil sous la coupole du Panthéon. Un pendule similaire peut être réalisé dans une cage d’escalier avec une masse de plusieurs kilogrammes et un fil d’au moins dix mètres (quelques heures d’oscillation seulement). Par rapport à un repère terrestre le plan d’oscillation du pendule tourne en 24h00 au Pôle Nord, en 31h48 à Paris, ne change pas à l’équateur.
6) « La déviation vers l’est » : Un corps en chute libre ne tombe pas suivant la verticale (Expérience tentée pour la première fois en 1860 dans un puits de mine à Freyberg (51° N) : 28 mm de déviation sur 158 m de chute.
7) « La déviation vers la droite » (vers la gauche dans l’hémisphère sud) d’une particule dont la vitesse est tangente à la Terre. On peut voir cette déviation dans les enroulements de nuages autour des dépressions (enroulement en sens trigonométrique dans l’Hémisphère Nord)
parue en janvier 1634 dans la Gazette de Théophraste Renaudot
[ ... ] Pour ce que dans l’une des conférences tenues en ce bureau le 24 d’octobre 1633, et avant que nous sachions ce qui en avait été décidé par le Saint-Siège, il fut discuté du mouvement de la terre; j’ai cru être obligé de vous mettre ici la sentence rendue le 22 juin dernier contre Galilée, I’auteur de cette opinion, mais qui n’a été publiée que vers la fin de cette année. Et ce, pour empêcher que désormais cette question ne soit plus controversée.
« Nous, Gaspar Borgia, du titre de Sainte-Croix en Jérusalem
Fr. Felice Sentivo dit d’Ascoli, du titre de Sainte Anastasie
Guido Bentivoglio, du titre de Sainte-Marie du peuple
Fr. Desiderio Scaglia dit de Cremone, du titre de Saint Charles
Fr. Antonio Barberino, dit de Saint Onofrio
Laudonio Zacchia dit de Saint Sixte, du titre de Saint-Pierre-des-liens
Berlingerio Geffi, du titre de Saint Augustin
Fabricio Vecospi, du titre de Saint Laurent in pane é penna, tous prêtres.
Francesco Barberino, du titre de Saint Laurent en Damas, et Mario Ginerti, de Sainte Maria Nova, diacres, par la miséricorde de Dieu, cardinaux de la S.R.E., et spécialement députés pour être inquisiteurs généraux de la Sainte Foy Apostolique.
Comme ainsi soit que toi Galilée, fils de Vincent Galilée, florentin, âgé de 70 ans, a été dénoncé dès l’an 1613 à ce Saint-Office, pour ce que tu tenais pour véritable la fausse doctrine enseignée par aucuns, que le Soleil soit le centre du monde, et immobile, et que la terre ne l’était pas, mais se remuait d’un mouvement journalier, que tu enseignais cette doctrine à tes disciples, et l’écrivais aux mathématiciens d’Allemagne, tes correspondants. Tu avais fait imprimer un livre des taches du Soleil, et publié d’autres écrits, contenant la même doctrine, qui est aussi celle de Copernic. Les Théologiens et Docteurs ayant trouvé cette opinion non seulement absurde et fausse en philosophie, mais du moins erronée en la Foi. En suite de quoi, dès le 29 février 1616, dans la Sacrée Congrégation tenue devant Sa Sainteté, il fut décrété que l’Éminentissime cardinal Bellarmin mettrait ordre que tu quitterais entièrement cette fausse opinion. A faute de quoi le Commissaire dudit office t’en ferait exprès commandement avec défense de l’enseigner jamais à aucun autre, ni de la soutenir, à peine de prison. En exécution duquel décret le jour ensuivant après bénignes et familières remontrances du dit cardinal Bellarmin à toi faites dans sa mai son, le dit commissaire assisté de Notaire et témoins, te fit les commandements et défense fut dite, auxquels ayant promis d’obéir, tu fus envoyé, et un décret fut fait par cette Congrégation, censurant les livres qui traitaient de telle doctrine contraire à la Sainte Écriture. Toutefois, il a naguère paru un livre imprimé à Florence sous ton nom, intitulé Dialogue des deux systèmes du monde de Ptolémée et de Copernic, auquel tu défens encore la même opinion. C’est pourquoi nous t’avons appelé de nouveau, et sur tes confessions, reconnaissances et productions, par sentence définitive rendue dans notre tribunal, du conseil et avis du R.P. Maître de lu Sacrée Théologie, et des Docteurs de l’une et l’autre Loi, après l’invocation du Saint Nom de Jésus et de la glorieuse Mère toujours Vierge. Entre le magnifique Carlo Sincero, Docteur ès-deux Lois, Procureur Fiscal de ce Saint-Office, demandeur et accusateur d’une part, et toi Galilée, accusé et ici présent, d’autre part. Disons, prononçons, et sentencions que toi, Galilée, tu t’es rendu fort suspect d’hérésie, ayant tenu cette fausse doctrine du mouvement de la terre et repos du soleil, et que l’on pouvait défendre comme probable une opinion après avoir été déclarée contraire à I’Écriture. Conséquemment, tu as encouru toutes les censures et peines des sacrés Canons, desquels néanmoins nous te délions, pourvu que dès maintenant, avec un cœur sincère et une foi non feinte, tu abjures, maudisses et détestes devant nous les susdites erreurs et hérésies, et toute autre erreur et hérésie contraire à l’Église. Et toutefois, afin que ta grande faute ne demeure tout à fait impunie, que tu sois plus retenu à l’avenir, et serves d’exemple aux autres, nous ordonnons que les dialogues susdits seront prohibés par édit public; que tu seras emprisonné dans les prisons dudit Saint-Office, à notre arbitre, et pour pénitence salutaire t’enjoignons de dire trois ans durant une fois la semaine les sept psaumes Pénitentiaux. Nous réservons la faculté de modérer, changer, ou lever en tout ou en partie les susdites peines et pénitences. »
A quoi ledit Galilée acquiesça le même jour, abjurant, maudissant et détestant la susdite erreur, de vive voix et par écrit dans le Couvent de Minerve. Et il promit à genoux, la main sur les Saints Évangiles, de n’aller jamais à l’encontre de la sentence susdite.
|
Chapitre 6 |
VI Repérage sur le globe (cycle 3) |
Savoir ce que représentent: Pôles, Équateur, Méridiens, Parallèles
Comprendre que c’est le mouvement de rotation qui donne aux pôles leur rôle particulier
points opposés de la Terre (P .Nord, P. Sud) sur son axe de rotation (polos en grec : pivot, axe du monde)
Les flèches Nord des cartes indiquent la direction du pôle Nord
Pôle Nord appelé aussi pôle arctique, pôle boréal, Pôle sud appelé aussi pôle antarctique , austral
Donner alors l’axe (brochette en bois)
Équateur: cercle équidistant des pôles; le tracer en mesurant avec un fil la distance des pôles et le diviser en deux pour l’équateur, en 4 pour les parallèles 45°N, 45°S
cercles gradués de 0° à 90°N (P. Nord), et 0° à 90°Sud (P. Sud): LATITUDE
demi-cercles joignant les pôles.
Il faut choisir une origine : ce sera celui qui passe par Greenwich. On gradue de 0° à 180°Est et 0° à 180° Ouest: LONGITUDE
Greenwich (0° ; 51°29’N) Lyon (4°49’E; 45°46’N) Paris (2°20’14”E; 48°50’11N)
Villes sur le même méridien que Lyon: Bergen en Norvège (5°E; 60°N), Phare d’Alger (3°E07’24”, 36°47’20”N), Île Bouvet près de l’Antarctique (5°E, 54°N), La Mecque (40°11’E, 21°21’N)
Une ville, une montagne, une mer où tu as envie d’aller
Coller un petit disque rond en carton matérialisant l’horizon de Lyon dessiner une petite flèche indiquant le Pôle Nord sur cet horizon
Dessiner une petite flèche notée Sud indiquant le Pôle Sud, une à 90° vers la gauche notée Ouest, une troisième vers la droite notée Est: cela s’appelle une rose des vents
Lieu donné, trouver son code Exemple: Islande Réponse: (20°O, 65°N)
Code donné, trouver le lieu Exemple: (140° E, 36 °N)? Réponse: Tokyo
Sa direction correspond à celle du soleil réel. On peut visualiser cette direction en allant dehors, voir sur les boules blanches les pays où le soleil se “lève”, où il se “couche”, où il est midi solaire. Regarder si les pôles sont dans la nuit, le jour.
|
Chapitre 7 |
Espace et diversité des paysages: Première découverte du globe, des éléments du cosmos. Observation du temps qu’il fait (données météorologiques et climatiques élémentaires)
Le temps dans la vie des hommes: Heure, journée, semaine, mois, a année, rythmes naturels et mesure sociale du temps. Utilisation et fabrication de calendriers
Monde du vivant: modification des milieux selon les saisons
Savoir que la rotation de la Terre sur elle-même est responsable de l’alternance des jours et des nuits
Comprendre que l’inclinaison et la fixité de l’axe des pôles par rapport à l’écliptique entraîne la variation de durée du jour et de la nuit. Savoir que la durée du jour et de la nuit dépend de la date, du lieu
Savoir modéliser un problème physique: ici celui de la variation de la durée du jour
Émettre des hypothèses, essayer de les valider
Sur le calendrier: repérage du début et de la fin de l’automne
Compter le nombre de mois, de semaines, de jours Repérer les fêtes
Heure de lever et coucher du soleil Dictons météo ou agricoles...
Sortie dans un parc: observation des arbres, des plantes
À partir de textes ou de photos: types de temps (brouillard, rosée); activités (vendanges, semailles, chasse); Transformations de la nature: a) oiseaux qui partent (hirondelles...), oiseaux qui restent b) fruits, légumes de l’automne
Commencer cette leçon le jour d’un changement de saison, et poser des questions sur la saison concernée: quand commence t-elle, quand finit-elle? (Quand commence l’automne?)
Les enfants donnent souvent des repères sociaux (rentrée des classes, changement d’heure...), liés à la végétation (les feuilles jaunissent et tombent, l’herbe ne pousse plus, les rameaux de certains arbres tombent...), météorologiques (froid, vent, pluie, ...) et rarement le critère astronomique lié à la définition des saisons et portant sur l’éclairement de la Terre et sur la durée du jour.
Il faut faire surgir ce critère, par des questions, par l’étude de documents (bulletin météo du journal local, calendrier du Lyonnais pour le mois concerné donnant les levers et couchers de soleil, la date des équinoxes et solstices...)
Première approche de la variation de durée du jour
Bulletin météo du journal, calendrier du mois
L’enseignant définit la saison concernée L’automne, par exemple, commence quand le jour en devenant plus court est égal à la nuit
L’hiver commence quand les jours s’allongent. Le printemps commence quand le jour en devenant plus long devient égal à la nuit
L’été commence quand les jours diminuent
Calendrier donné par l’enseignant des levers et couchers à Lyon
Lecture et commentaires Diagramme d’évolution
Trouver la date et la durée du jour le plus court, le plus long; la date des jours où “nuit = jour = 12 heures”
Avec lampe de poche (soleil) et boule blanche (Terre), chercher pourquoi la durée des jours varie
Demander d’abord de positionner la boule pour un jour de solstice ou d’équinoxe, passer dans les groupes
L’enseignant avec une grosse lampe de 200 W résume les différentes démarches proposées par les enfants et réfute les solutions qui conviennent souvent partiellement, mais que des éléments nouveaux réfutent (L’étoile du bout de la petite Ourse, polaire, reste fixe), argument physique sur la stabilisation par rotation (assiette tournant sur baguette, vélo, gyroscope...)
Choisir un plan d’orbite terrestre, placer le globe aux solstices et équinoxes
Bien montrer que ces événements arrivent à un instant précis (jour, heure, min, s)
L’axe des pôles est incliné sur le plan de l’orbite terrestre et garde une direction fixe par rapport aux étoiles ce qui explique l’inégalité des durées du jour et de la nuit durant l’année
Quand fait-il le plus chaud, le plus froid? Pourquoi? Les deux paramètres : durée d’ensoleillement et inclinaison des rayons
Calcul de la durée de l’année des saisons. Équinoxes: 20 mars 2000 à 7h35, 20 mars 2001 à 13h31, 20 mars 2002 à 19h16, 21 mars 2003 à 1h00, 20 mars 2004 à 06h48, 20 mars 2005 à 12h33, 20 mars 2006 à 18h25
 Lyon, le 21 décembre
Lyon, le 21 décembre
 Lyon, le 21 mars et 22 septembre
Lyon, le 21 mars et 22 septembre
 Lyon, le 21 juin
Lyon, le 21 juin
|
Chapitre 8 |
Élaborer, construire et utiliser un instrument de mesure du temps
Comprendre l’heure solaire et constater la différence avec l’heure légale (sans commentaires pour l’instant)
Observer la régularité du mouvement apparent du soleil
 Rappels
RappelsQuelle heure est-il?
Que veut dire cette expression?
Cite des instruments de mesure du temps : horloge, bougie de notaire, chronomètre, clepsydre, sablier, montres diverses..
Peut-on connaître l’heure sans instrument moderne?
Le saladier montre la trajectoire apparente régulière contenue dans un plan incliné par rapport à l’horizon (44° à Lyon: 90° - latitude): si on observe par rapport à une Terre correctement positionné (voir cadran solaire de Ternay)

Photo II‑1: Cadran de Ternay (Rhône) aux solstices et équinoxes
Ce plan est // à l’équateur terrestre et s’appelle l’équateur céleste
Peut-on utiliser ce résultat pour faire un instrument de mesure du temps
Le « saladier » est la réplique du polos grec qui a permis aux Anciens de comprendre les phénomènes célestes et la géographie terrestre.
Il constitue un outil pédagogique de grande valeur
En combien a t-on divisé la durée séparant deux passages du soleil au méridien? Réponse: 24
En combien allons nous diviser notre cadran? Réponse: 24. Il y a une différence avec une horloge où la petite aiguille fait 2 tours en 24h d’où 12 graduations
Analogie: ombre = aiguille de l’horloge
graduations du cadran solaire = graduations du cadran de l’horloge
cadran le plus simple = bâton (gnomon) en terre
Cadran placé sur le sol au pôle Nord du globe (il est plus facile de comprendre en plaçant la Terre un 21 juin) Impression de l’Esquimau: il voit l’ ”aiguille” tourner sur le cadran.
Impression d’un observateur ne tournant pas avec la Terre: il voit l’ ”aiguille” fixe et le cadran tourner
Les graduations sont-elles régulières si la Terre tourne régulièrement? (Réponse: OUI)
Quel est l’angle représenté par 1h? (Réponse: 24h --- 360° donc 1h--- 360/24=15°)
Un Lyonnais peut-il prendre exemple sur l’Esquimau pour construire son cadran?
Construction d’un cadran équatorial placé à Lyon Mise en station. Lecture de l’heure solaire
Constat: Différence avec l’heure de notre montre appelée “heure légale en France”
Prévoir: l’heure de récréation ou du goûter...
Apports du maître: 2 problèmes sont soulevés par un cadran horizontal avec un bâton vertical:
* “petit” problème”: les graduations sont irrégulières (elles ne le seront pas dans le cadran équatorial, mais le seront dans le cadran horizontal ou vertical à style orienté vers l’Étoile Polaire)
* “gros” problème: une direction donnée n’indique pas une heure donnée (dépend du jour de l’année)
On peut visualiser sur l’ensemble des relevés de l’année le point de concours des droites horaires et incliner le gnomon à partir de ce point suivant l’axe de rotation apparent du soleil donné par le saladier

Observer sur chaque photo: place du style, position et orientation de la table de lecture, graduations
|
Chapitre 9 |
Connaître trois systèmes de repérage dans le temps Heure Solaire, Heure Légale, Temps Universel Comprendre l’aspect conventionnel mais nécessaire de l’Heure Légale
NOTION DE MESURE: pour mesurer une grandeur il faut un instrument, une origine, une unité
INSTRUMENT: Le cadran solaire
ORIGINE: Mi-di = le milieu du jour
à cet instant l’ombre est * sur le méridien * la plus courte
UNITE: Jour solaire = Durée séparant 2 Mi-dis consécutifs
Problème : Est-il midi solaire en même temps pour tout point de la Terre?
« Remède »: Convention Internationale de Rome (1883)
Création de 24 fuseaux de 15°
Heure Légale = Heure solaire du méridien central du fuseau + E
Exemple: Espagne et Portugal
Exception: France presque centrée sur le fuseau 0 mais s’alignant sur fuseau +1 en hiver, +2 en été
Numérotation: Vers l’Est +1, +2, +3... Vers l’Ouest -1, -2, -3...
Temps Universel (T.U. ou U.T.)
Heure Légale du fuseau 0 = Heure Solaire de Greenwich + E
= Heure Solaire Moyenne de Greenwich
Sur l’heure légale
Sur le passage de l’heure légale à l’heure solaire
|
CHAPITRE 10 |
Connaître la course du soleil en une journée et à différentes dates.
Réaliser et exploiter des mesures.
Relier ces observations au cycle des saisons vu antérieurement
Il y a un problème, il faut réaliser des observations précises et faire des mesures
Ombre du gnomon aux solstices et équinoxes
Retrouve t-on la notion de saison? Les deux aspects ?
En été le soleil est présent plus longtemps au-dessus de l’horizon.
En été le soleil est plus haut: le sol s’échauffe plus.
Gommettes sur un demi-ballon transparent
trajectoire apparente du soleil
|
11 |
XI La Lune |
Cycle 1: Vivre ensemble, agir dans le monde, découvrir le monde, imaginer, sentir, créer
activités graphiques, repérage dans l’espace
Cycle 2: Première découverte du globe, des éléments du cosmos. Le temps dans la vie des hommes
Cycle 3: Le système solaire et l’univers, l’aventure spatiale
Démarche scientifique pour le cycle 3: remettre ses idées en question, se poser des questions, trouver des éléments de réponse (en formulant des hypothèses, avec des expériences ou observations...)
Cycle 1 et 2: observer * le mouvement diurne * le changement d’apparence de la Lune au fil des jours
Cycle 3: savoir utiliser une maquette en trois dimensions du système Terre - Lune - Soleil
savoir passer “d’une vision sur Terre à une vision d’extraterrestre”, changer de repère
Comportement: travailler par groupe, s’exprimer
Dessine la Lune
Quand est -elle visible?
Dépouillement
Différents problèmes à résoudre et nécessité d’observer
Dessin de la Lune sur un même paysage à 8h30 et 11h30 (si on commence en premier quartier)
Résultats: la Lune est visible de jour, elle garde la même apparence un même jour mais possède un mouvement apparent comme le soleil, elle est éclairée du côté du soleil
dessin de l’apparence de la Lune une seule fois par jour avec date, lieu, heure de l’observation
indiquer la direction du soleil/ côté éclairé de la Lune
Tout le monde observe la même chose le même jour
Le soleil est toujours du coté éclairé de la Lune
Il y a un cycle d’apparition des phases de 29 à 30 jours environ (29j 12h 44mn)
Réalisation d’une frise chronologique des phases, écrire ou faire trouver le nom des phases
Réaliser une maquette Que demandent les enfants pour leur maquette? (assiette ronde, croissant, plusieurs « Lunes », diverses lampes de poche, ampoule centrale puissante...)
A l’extérieur un jour où la Lune est visible: “Pêche à la Lune”
En classe par groupe de deux enfants
lampe de 200 W au centre, des boules blanches pour la Terre et la Lune, retrouver les observations
Regroupement avec le maître
lampe de 200 W au centre, globe terrestre autour duquel se rassemblent les enfants, et une boule blanche (Lune) qui tourne autour du globe
La Lune est une sphère
La Lune est éclairée par le Soleil
La Lune tourne autour de la Terre en 29,5 jours, sur un plan incliné par rapport au plan de l’écliptique
C’est parce que nous regardons la Lune de la Terre que nous voyons des phases
Maquette dans la cour
Tracé de l’ellipse de la trajectoire lunaire, enfants autour, placer la Lune du jour/soleil, la faire circuler
Dans la cour “danse Terre-Lune” autour du Soleil
Exercices sur feuilles avec petites boules
Divers exercices:
Le Soleil a rendez-vous avec la Lune
La face cachée de la Lune
Les jardiniers: la Lune montante et descendante; la Lune rousse
Les marées
La Lune cendrée
Le « lunoscope »
La date de Pâques, les mois musulmans ou hébreux
Histoire de la conquête de la Lune
Étude de diapositives, vidéos, documents écrits ou photos
Règles mnémotechniques valables dans l’hémisphère Nord
Étude du calendrier des Postes
Les éclipses
A l’aide d’une maquette trouver les heures approximatives de visibilité des phases
|
Chapitre 12 |
Repérage sur la terre
Rotation de la terre sur elle-même et jour et nuit
Révolution de la terre autour du soleil et saisons
Dessine ce que tu peux voir dans le ciel, la nuit.
Qu’est-ce qu’une constellation?
Donne les noms de celles que tu connais.
Combien voit-on d’étoiles à l’œil nu?
Document 1: Que représente t-il? Cherche des formes connues et trace-les.
Document 2: Trouve la place de chaque figure sur le document 1.
Document 3: Intérêt des constellations. Dimension angulaire
Clefs du ciel: à partir de la grande Ourse: Étoile Polaire, Lion, Arcturus dans le Bouvier, Castor et Pollux, Bételgeuse dans Orion.
Globe terrestre et ballon jaune pour le soleil
Rotation de la terre autour de l’axe des pôles: Dans quel sens? Le faire retrouver
Révolution autour du soleil: Dans quel sens? On le donne
Placer le bonhomme à Lyon sur le globe, placer le ballon-Soleil
Faire tourner la Terre sur elle-même
Quand est-il midi (milieu du jour) solaire à Lyon, minuit solaire, 6h solaire, 18h solaire?
Le plan de l’écliptique représente le plan de la trajectoire de la terre autour du soleil
Durant une journée, le soleil ne bouge pas par rapport aux étoiles
Il a un mouvement apparent par rapport aux constellations de l’écliptique au cours de l’année et il revient à la même place au bout d’un an.
Comparaison du globe céleste au globe terrestre: Pôles (étoile polaire proche du pôle céleste Nord), équateur céleste, parallèles et méridiens célestes
Cercle écliptique: trajectoire apparente du soleil au cours de l’année (trajectoire apparente approximative de la lune et des planètes)
Latitude: oui la carte construite sera valable pour la latitude 45°N
Longitude: non, deux lieux différents verront le même ciel à une heure solaire locale donnée
Oui et bien observer que c’est l’heure solaire qui compte: un habitant de Lyon à minuit solaire de Lyon observera le même ciel qu’un habitant de Montréal à minuit solaire de Montréal
Par exemple: à quelle heure le ciel du 21 juin, correspond-il au ciel du 21 mars à 24h? Réponse: 18h
+3 mois de décalage¤-6 heures donc +1 mois ¤-2 heures
Observation des constellations (lettres majuscules), des étoiles (lettres minuscules), de l’équateur céleste, du cercle écliptique, de l’étoile polaire, du pôle céleste
Expliquer qu’il s’agit d’une projection du globe céleste sur un plan en regardant au-dessus de sa tête.
On pourrait graduer ce fond étoilé en “longitude céleste” comme sur la terre avec des degrés (Les astronomes graduent en ascension droite exprimée en heure comme unité d’angle). Comme le soleil parcourt la voûte étoilée en 365,25 jours, on choisit de diviser le pourtour en 365,25 parties et de d’indiquer la position du soleil ce jour. (Pour le maître: Le soleil se trouve en fait à l’intersection équateur-écliptique à l’instant des équinoxes et il y a léger déplacement des graduations par rapport au fond étoilé d’une année sur l’autre)
Pourquoi la terre n’est-elle pas placée?
Pourquoi le soleil n’est-il pas placé? On place le soleil le jour de l’observation...
Pourquoi lune et planètes ne sont-elles pas placées?
Voit-on toutes ces étoiles en même temps? Réponse non; donc il faut un cache que l’on fera tourner en fonction de l’heure. Ce cache ne dépendra que de la longitude de l’observateur
Pourquoi les points cardinaux sont-ils inversés? Placer la carte au-dessus de sa tête...
La forme ovale limite les étoiles visibles et représente la ligne horizon: parcourir avec son bras le pourtour de l’horizon puis avec son doigt le pourtour de l’ovale.
Le zénith est au milieu de l’ovale: le montrer avec son bras, puis le pointer sur le tympan
La ligne d’azimut Est-Ouest est représentée par une ligne courbe: la parcourir avec son bras dans l’espace puis la suivre du doigt sur le tympan
On peut choisir de graduer la ligne d’horizon de 0° à 360°. On peut aussi choisir de graduer la voûte céleste en 24 graduations à partir du méridien céleste nord (0h et 12h au sud)
On découpe le tympan (ovale et entre 17h et 7h) et le fond étoilé
Positionner le fond étoilé lorsque le soleil passe au sud (derrière le tympan): on constate que cela correspond à la graduation spatiale 12h qui correspond aussi à l’heure solaire de passage du soleil. Si on fait tourner régulièrement le fond étoilé, les graduations spatiales vont aussi correspondre à l’heure solaire d’observation du ciel donc à des repères temporels.
Dans quel sens faut-il tourner le fond étoilé?
Persée, Andromède, Céphée, Cassiopée, La Baleine, Pégase
Hercule, L’aigle, Le Cygne, Dragon, Lion, Taureau, La Flèche
Orion, Le Scorpion...
Saint Jacques de Compostelle
Les constellations qui quadrillent le ciel ont été élaborées par les astronomes pour se repérer sur la terre en trouvant l’étoile polaire et donc le nord, pour repérer lune, planètes et comètes, et à se repérer dans le déroulement des saisons en observant la position du soleil (ciel = atlas + calendrier)
Elles regroupent des étoiles apparaissant dans la même zone du ciel mais que l’on sait depuis 1838 être à des distances très différentes.
En 1930 l’Union Astronomique partage la voûte céleste avec 88 constellations.
L’observation des mouvements des astres puis l’analyse du message complexe transmis par la lumière ont permis à l’homme de mieux comprendre l’Univers qui l’entoure.
|
Chapitre 13 |
Compétences : Exploiter des documents, utiliser des notions mathématiques (maquette, échelle, proportionnalité)
Connaissances …
Connais-tu d’autres objets célestes que le soleil, la lune et les étoiles?
Si oui, nomme-les et fais un dessin où ils apparaissent.
En quoi n’est-ce pas une vraie photo? Placer le soleil, les planètes.
Quelle est la trajectoire des planètes? Compte-les. Nomme-les
Mercredi Viendras-Tu Manger Avec Jean Sur Une Nappe Propre?
Intérêt Échelle 1 / 10 000 000 000
Maquette dans la cour (étoile la plus proche à 4000 km)
Expliquer pourquoi Vénus est appelée « étoile du berger »
Planètes visibles à l’œil nu: Mercure, Vénus, Mars, Jupiter, Saturne
1) Déplacement des planètes / constellations au fil des jours
alors que les étoiles ne se déplacent que plus lentement vu de la Terre
2) Les planètes sont « proches » du soleil: Terre-Soleil = 8mn Lumière Soleil-Pluton=6 H.L.
alors que Soleil - Proxima du Centaure = 4 A.L.
3) Les étoiles émettent leur propre lumière car très chaudes (fusion nucléaire)
alors que les planètes renvoient la lumière du soleil
1) À l’œil nu: points lumineux (au télescope: petit cercle pour les planètes)
2) Mouvement diurne de rotation / étoile polaire
Résumé : Les planètes paraissent semblables aux étoiles lorsqu’on regarde le ciel nocturne. Mais au fil des semaines on les voit se déplacer plus ou moins rapidement par rapport aux constellations (planète = “étoile vagabonde”), ce qui les rendaient autrefois mystérieuses. On sait maintenant que ce sont des astres qui tournent autour du soleil et renvoient sa lumière alors que les étoiles qui sont très chaudes et très loin émettent leur propre lumière.