Further work on extending the multipartite method has led to the HOTBM method, available in the FloPoCo project
Multipartite methods can be obtained from FloPoCo by requesting a HOTBM operator of degree 1. The advantages of using FloPoCo are smaller operators if you are ready to use multipliers, and also a better interface where you can type in any function without having to edit the code.
Development now goes to FloPoCo but this is still work in progress: by using the multipartite code below, you may get a better optimized operator in less time.
The purpose of this page is to provide a reference implementation of the Multipartite Method for Function Evaluation presented in the 15th IEEE Symposium on Computer Arithmetic (an earlier version is available as INRIA research report RR-4059). These articles report results obtained using the software distributed here. These articles also include an description of the multipartite method which is as accurate as possible. The source files distributed here are intended to be an description which is even more acurate.
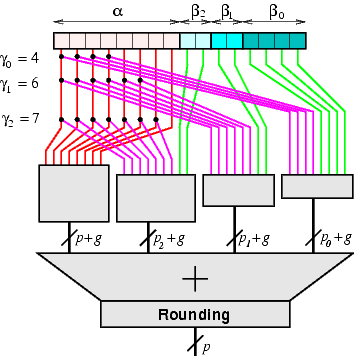
The Multipartite Method derives architectures for the evaluation of arbitrary continuous functions, for precisions between 8 and 24 bits, with faithful rounding. The architectures consist of tables and adders (see the figure below). They are much smaller than a simple table implementation of the function. For example, a 16-bit sine function can be implemented in 8,960 bits of memory and a 4-input adder, instead of a single table of 1,048,576 bits. This is a reduction by a factor of 100 in area. Besides, the architectures lend themselves to efficient pipelining.

This program is available in the form of a java archive containing the source and compiled classes.
To lauch the program, type java -jar Multipartite2-2-vhdl.jar or double-click on it if your system allows.
This opens a window where you can chose a function among a few predefined functions, chose the input and output precisions (between 2 and 24), and chose the number of tables that will be used (between 1 and 5, start with 2).
Clicking on Start lauchs the computation of the optimal architecture. When the computation is done, a second window opens showing the values of the various parameters (see the figure above for a description of these parameters). These parameters are set up to an initial near-optimal value: It is not always optimal in the sense that sometimes, the various sources of errors may compensate one another. You can therefore usually improve the table size by a few percents by finetuning these parameters. The Exhaustive Check button tests exhaustively the abstract architecture and report the worst-case error in terms of LSB.
In this second window, the VHDL button outputs VHDL code.
Please contact us (address at ens-lyon.fr) and tell us what function/precision/application you are interested in.
The source code of the method is distributed under the GPL. Unpack this archive by jar -xvf to see the source files.
You may want to
Don't hesitate to contact us (address at ens-lyon.fr) for more details.
This program has been developped and tested using java 1.2.2 , 1.3.1 and 1.4.2.
This program is distributed under the GPL. See inside the archive for details.