|
|
ROMAResource Optimization:
|
- Application resilience
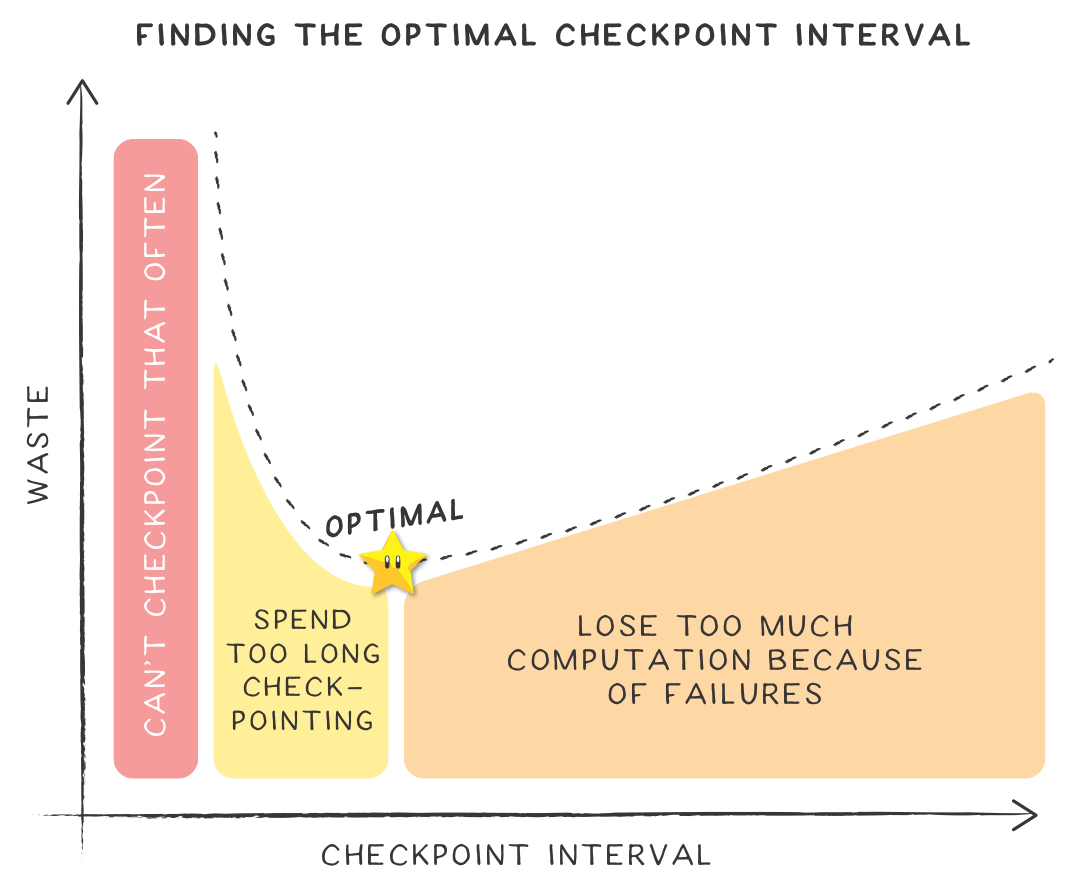
Most powerful supercomputers are victim of more than one failure per day. Resilience is the ability, for an application, to produce a correct result in spite of faults. Among fault-tolerance protocols and techniques, we aim at predicting which is the best one for a given application and a given platform. We rely on modelization, probabilistic analyzes, and discrete event simulations. - Multi-criteria scheduling strategies
We mix user-oriented objectives (time-to-solution, throughput, etc.) with platform-oriented constraints (energy, memory, etc.) when designing scheduling strategies that finely take into account platform characteristics beyond classical ones (like the computing speed of processors and accelerators).
- Solvers for sparse linear algebra and related optimizations problems
We work on most aspects of direct multifrontal solvers for linear systems, usually in the scope of the MUMPS solver we co-develop. We also work on combinatorial scientific computing, that is, on the design of combinatorial algorithms and tools to solve combinatorial problems, such as those encountered, for instance, in the preprocessing phases of solvers of sparse linear systems.
Main collaborations: Georgia Tech; INPT-IRIT, Toulouse; Joint Laboratory on Extreme Scale Computing; University of Tennessee, Knoxville.