Publication du RDP dans la revue PNAS, le 21 novembre 2023. Communication du CNRS Ingénierie du 7 décembre 2023.
Un écoulement d'eau sur des roches solubles peut créer des motifs constitués de multiples cuvettes bordées de crêtes acérées. En combinant des mesures de terrain, un modèle numérique et des expérimentations en laboratoire, une équipe menée par le laboratoire MSC (CNRS/Université Paris Cité), en collaboration avec le LPG (CNRS/Nantes Université/Université d'Angers) et le RDP (CNRS/ENS de Lyon/Inrae) a montré que l’apparition de ces formes résulte d’un mécanisme géométrique. Les résultats sont publiés dans la revue PNAS.
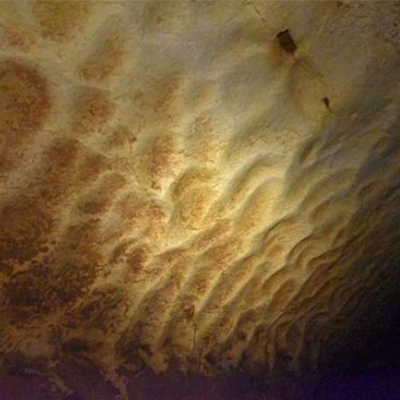
Dans les grottes créées par des rivières souterraines, on observe des motifs remarquables creusés sur les parois calcaires : de multiples cuvettes entourées de crêtes acérées, dont la taille peut varier de quelques centimètres à plusieurs mètres. Ces structures, appelées ''coups de gouge'', ou ''scallops'' en anglais, résultent de la dissolution de la roche en présence d'un écoulement d'eau. Une équipe du laboratoire Matière et systèmes complexes (MSC, CNRS/Université Paris Cité), en collaboration avec le Laboratoire de planétologie et géosciences (LPG, CNRS/Nantes Université/Université d'Angers) et le laboratoire Reproduction et Développement des Plantes (RDP, CNRS/ENS de Lyon/Inrae), a montré que l'émergence naturelle de ces formes s'explique par un mécanisme purement géométrique.
L'étude a démarré par une observation sur le terrain, dans la grotte de Saint-Marcel (Ardèche), dont les parois comportent de spectaculaires motifs du type ''coups de gouge''. Par une technique de photogrammétrie (mesures dimensionnelles à partir de multiples prises de vue photographiques), une reconstruction 3D de l'une des parois a pu être réalisée. Ces mesures ont permis de caractériser précisément la taille, la forme, ainsi que les variations de courbure des motifs, et en particulier de mettre en évidence l'existence de singularités: des crêtes acérées dont la courbure est quasi infinie. Comme il est impossible d'observer directement la formation de ces motifs, qui s'étend sur plusieurs milliers d'années, l'équipe a cherché à en élucider le mécanisme en s'appuyant sur un modèle de simulation numérique et sur des expérimentations en laboratoire. Un modèle simple d'érosion par dissolution montre que la surface d'une roche soluble qui présente initialement des variations de courbures (des ondulations), lorsqu'elle est soumise à une ablation dont la vitesse est perpendiculaire à la surface, donne en effet naissance à des motifs composés de cuvettes bordées de crêtes pointues. Ce phénomène géométrique ne dépend pas du matériau de la roche, et se produit à la seule condition qu'il existe dans l'écoulement une forme d'instabilité, qui crée des variations du taux de dissolution.
Pour tester la validité de ce modèle, des expériences de dissolution par convection ont été menées, en plongeant des blocs de matériau soluble (sel) dans un aquarium rempli d'eau. La topographie de la surface de dissolution a été mesurée périodiquement par profilométrie laser, avec une précision d'un dixième de millimètre. Le même type de motifs typiques a pu être observé, avec des résultats conformes à ceux donnés par le modèle numérique. Pour approfondir ces résultats, l'équipe du MSC a démarré une nouvelle série d'expérimentations plus proche des conditions naturelles d'érosion dans les grottes, en étudiant le phénomène d'érosion par dissolution dans un canal parcouru par un courant d'eau. Par ailleurs, le même type de mécanisme géométrique peut expliquer d'autres types de motifs remarquables produits par ablation, comme ceux observés lors de la fonte de la face immergée des icebergs, ou de la sublimation des glaciers de haute-altitude, ou encore sur des météorites après leur rentrée dans l'atmosphère terrestre.
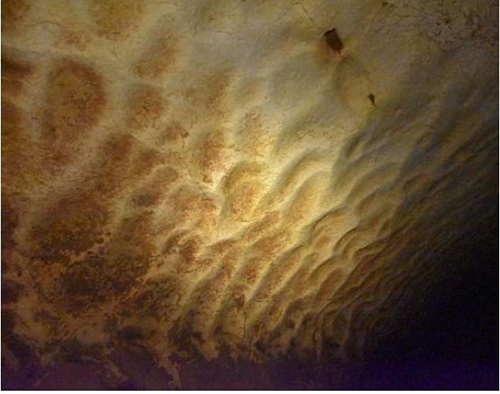
© Martin Chaigne, Sabrina Carpy, Marion Massé, Julien Derr, Sylvain Courrech du Pont, et Michael Berhanu

© Martin Chaigne
Référence
Emergence of tip singularities in dissolution patterns. YMartin Chaigne, Sabrina Carpy, Marion Massé, Julien Derr, Sylvain Courrech du Pont et Michael Berhanu. PNAS, 21 novembre 2023.
DOI : 10.1073/pnas.2309379120
Archive ouverte ArXiv : arXiv.2306.11676
Archive ouverte HAL : hal-04316918, version 1
Mots clés






