
Publication du Laboratoire de Physique dans la revue Nature, le 14 juin 2023. Communication du CNRS-INP du 14 juin 2023.
Une équipe de recherche impliquant des membres du Laboratoire de Physique de l'ENS de Lyon a montré l’existence d’une nouvelle forme d’ordre encore jamais identifiée dans la nature : l’ordre "non-orientable" qui peut doter des structures simples de propriétés leur permettant de stocker de l’information. Des travaux publiés dans la revue Nature.
Qu’il s’agisse de la cristallisation, de la formation des troupeaux d'animaux ou de l’apparition d’une aimantation dans un matériau magnétique, l'émergence de l'ordre dans la nature est expliqué par un concept universel formalisé par Lev Landau dans les années 50. Ce concept est connu sous le nom de brisure spontanée de symétrie. L’exemple le plus standard est celui des liquides qui se transforment à basse température en cristaux. Les liquides sont parfaitement homogènes et isotropes, en cela qu’ils restent inchangés sous l’effet des toutes les translations et rotations possibles. A l’inverse, les cristaux sont ordonnés périodiquement et brisent les symétries de translation et de rotation des liquides selon des directions arbitraires qui se renouvellent totalement à chaque recristallisation.
Dans certains cas néanmoins, l’ordre émergent est frustré. Une collaboration réunissant des chercheuses et chercheurs du Laboratoire de physique de l’ENS de Lyon (LPENSL, CNRS/ ENS de Lyon) et de l’Université d’Amsterdam vient d’étudier théoriquement et expérimentalement les propriétés de matériaux dont la topologie empêche la réalisation globale d'une phase ordonnée. Ces situations sont typiquement observées dans les systèmes ayant la structure d’un cercle où d’un tore, c’est-à-dire des topologies où existent des courbes fermées encerclant des trous. Cette situation peut être illustrée par un exemple simple, celui de la structure mécanique montrée sur la figure A. Cette chaîne de losanges, quand elle est soumise à une compression homogène, se déforme en faisant tourner les losanges adjacents dans des directions opposées. Quand elle est constituée d’un nombre impair de losanges, cet ordre alterné est frustré : au moins une paire de losanges est contrainte à tourner dans la même direction. De façon remarquable la réponse mécanique de cet objet est identique à celle d’un ruban de Möbius mis lui aussi en compression (figure B). La topologie non orientable du ruban, avec cette impossibilité d’y distinguer deux faces distinctes, empêche de même le ruban de bomber de façon uniforme.
En se servant de cette analogie directe entre mécanique des surfaces non orientables et déformations de matériaux artificiels, les chercheurs ont réalisé également des structures toriques déformables (figure C) qui s’organisent pour mimer des déformations de surfaces non-orientables impossibles à visualiser dans notre monde à trois dimensions. Pour illustrer la richesse et les applications potentielles de ces systèmes dotés de ce que l’on nomme maintenant un ordre non-orientable, ils ont montré comment utiliser cet ordre topologique pour stocker de l’information dans ces déformations d’origine mécanique, ouvrant la voie à des applications potentielles dans le domaine des matériaux innovants à toutes les échelles, du mètre au nanomètre. Ces résultats sont publiés dans la revue Nature.
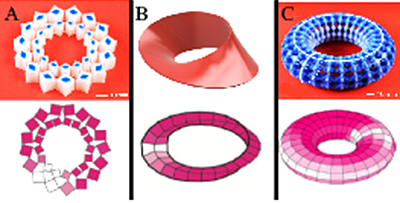
© Xiaofei Guo, Marcelo Guzman, David Carpentier, Denis Bartolo, Corentin Coulais
Référence : Non-orientable order and non-commutative response in frustrated metamaterials. Xiaofei Guo, Marcelo Guzman, David Carpentier, Denis Bartolo, Corentin Coulais. Nature, 14 juin 2023.
DOI : 10.1038/s41586-023-06022-7
Archive ouverte arXiv : 10.48550/arXiv.2111.13933
Structures
Disciplines
Mots clés






